Triangles

Home / Boards / CBSE / Important Questions / Class 10 / Maths / Triangles

Class 10 Math Chapter 6
Triangles
Important Questions

Q: Q.3 What are the six main types of triangles in mathematics, and how are they defined?

Ans: The six main types of triangles in mathematics are: Scalene Triangle: A scalene triangle has all three sides of different lengths, and all three angles are also different Isosceles Triangle: An isosceles triangle has two sides of equal length, and consequently, two angles are also equal. Equilateral Triangle: An equilateral triangle has all three sides of equal length, making all three angles equal to 60 degrees. Acute Triangle: An acute triangle has all three angles less than 90 degrees. Obtuse Triangle: An obtuse triangle has one angle that is greater than 90 degrees. Right Triangle: A right triangle has one angle precisely equal to 90 degrees.

Here are some important questions for Class 10 Mathematics Chapter 6, Triangles, carefully selected to help students prepare for the CBSE Class 10 Mathematics Examination in 2024-25. These questions cover various types of problems and are designed to assist students in understanding Triangles better. By practicing these diverse question types, students can clarify any doubts they may have and improve their problem-solving skills, leading to better performance in the chapter on Triangles.

Table of Contents

Introduction

In Chapter 6 of Class 10 Mathematics,Triangles, We will learn about the significance of corresponding angles and corresponding sides in establishing the similarity between triangles. Along the way, we will discover the beauty of geometric proofs and explore how to apply them to establish the similarities between triangles.

What are Triangle?

A triangle is a closed, three-sided polygon. Its basic properties include:

The sum of the interior angles of a triangle is always 180 degrees.
The sum of any two sides of a triangle is always greater than the length of the third side (Triangle Inequality Theorem).
The longest side of a triangle is opposite the largest angle, and the shortest side is opposite the smallest angle.

Class 10 Triangles Important Questions and Answers

Q1. In ΔPQR, if PS is the internal bisector of ∠P meeting QR at S and PQ = 15 cm, QS = (3 + x) cm, SR = (x – 3) cm and PR = 7 cm, then find the value of x.

Options

(a) 2.85 cm
(b) 8.25 cm
(c) 5.28 cm
(d) 8.52 cm

Ans. (b)

Explanation:
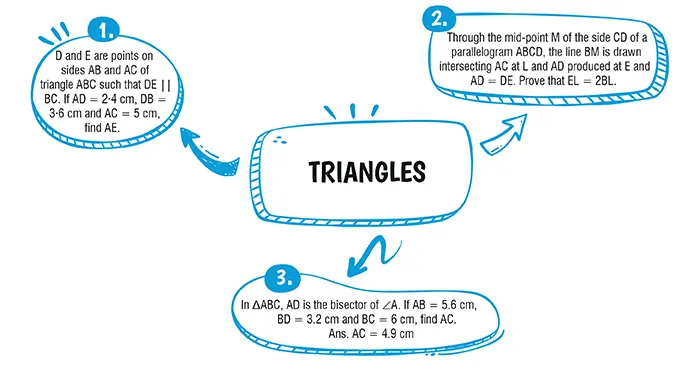
Since PS is the internal bisector of ∠P and it meets QR at S image.

\therefore \space\space\space\space\space \dfrac{PQ}{QS}=\dfrac{PR}{SR} \\[4.5 bp] \Rightarrow\space\space\space\space\space \dfrac{15}{3+x}=\dfrac{7}{x-3} \\[4.5 bp] \Rightarrow\space\space\space\space\space 7(3+x)=15(x–3) \\[4.5 bp] \Rightarrow\space\space\space\space\space 21+7x=15x – 45 \\[4.5 bp] \Rightarrow\space\space\space\space\space 15x–7x=45+21 \\[4.5 bp] \Rightarrow\space\space\space\space\space 8x=66 \\[4.5 bp] \Rightarrow\space\space\space\space\space 4x=33 \\[4.5 bp] \Rightarrow\space\space\space\space\space  x=8.25cm

Q2. In the figure given below, ABC is a triangle. BC is parallel to AE. If BC = AC, then what is the value of ∠CAE?

Options

(a) 20°
(b) 30°
(c) 40°
(d) 50°

Ans. (d)

Explanation:
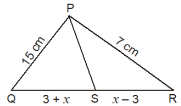
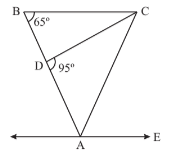
Given that, BC || AE
∠CBA + ∠EAB = 180°
⇒ ∠EAB = 180° – 65°
= 115°
BC = AC
Hence, DABC is an isosceles triangle.

⇒ ∠CBA = ∠CAB
= 65°
Now, ∠EAB = ∠EAC + ∠CAB
⇒ 115° = x + 65°
⇒ x = 50°.

Q3. D and E are points on sides AB and AC of triangle ABC such that DE || BC. If AD = 2·4 cm, DB = 3·6 cm and AC = 5 cm, find AE.

Explanation:
Given, DE || BC, AD = 2.4 cm, DB = 3.6 cm and AC = 5 cm

In ΔABC, DE || BC

\therefore \dfrac{AD}{DB}=\dfrac{AE}{CE} \\[4 bp] \text{[by basic proportionality theorem]} \\[4.5 bp] \Rightarrow \dfrac{AD}{DB}=\dfrac{AE}{AC-AE} \\[5 bp] \Rightarrow \dfrac{2.4}{3.6}=\dfrac{AE}{5-AE} \\[5 bp] \Rightarrow \dfrac{2}{3}=\dfrac{AE}{5-AE} \\[5 bp] \Rightarrow 3AE + 2AE = 10 \\[5 bp] \Rightarrow AE = \dfrac{10}{5} \\[5 bp] \Rightarrow AE = 2 cm

Q4. Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC at L and AD produced at E and AD = DE. Prove that EL = 2BL.

Explanation:
In ∆BMC and ∆EMD, we have

∠1 = ∠2 [Vertically opposite angles]

MC = MD [M being the mid-point of CD]

∠BCM = ∠EDM [Alternate angles]

Thus ∆BMC ≅ ∆EMD [by ASA] $\\ \Rightarrow BC = DE (cpct)$

Again, BC = AD [Opposite sides of the parallelogram ABCD] $\\ \therefore BC = AD = DE$

So, AE = AD + DE = 2BC …(i)

Again, in ∆AEL and ∆CBL, ∠5 = ∠6 [Vertically opposite angles]

∠3 = ∠4 [Alternative angles]

So, ∆AEL ~ ∆CBL

\\ \therefore \dfrac{EL}{BL}=\dfrac{AE}{BC}=\dfrac{2BC}{BC}=2

[From (i)]

Thus, EL = 2BL.

Q5. In ΔABC, AD is the bisector of ∠A. If AB = 5.6 cm, BD = 3.2 cm and BC = 6 cm, find AC.

Explanation:
Given, AD is the bisector of ∠A.
Thus, ∠BAD = ∠CAD
Now BC = BD + DC

⇒ 6 = 3.2 + DC ⇒ DC = 2.8 cm
⇒ 6 = 3.2 + DC
⇒ DC = 2.8 cm
Since AD is the angle bisector of ∠A,

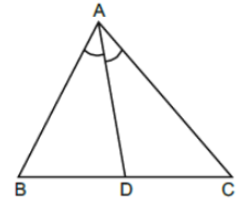
Hence $\\ \dfrac{DB}{DC}=\dfrac{AB}{AC} \space \space \text{[Angle bisector theorem]} \\[4.5 bp] \Rightarrow \dfrac{3.2}{2.8}=\dfrac{5.6}{AC} \\[4.5 bp] \Rightarrow AC = \dfrac{5.6×2.8}{3.2} = 4.9\space cm.$

CBSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Real Numbers
Chapter 2	Polynomials
Chapter 3	Pair of Linear Equations in Two Variable
Chapter 4	Quadratic Equations
Chapter 5	Arithmetic Progressions
Chapter 6	Triangles
Chapter 7	Coordinate Geometry
Chapter 8	Introduction to Trigonometry
Chapter 9	Some Applications of Trigonometry
Chapter 10	Circles
Chapter 11	Areas Related to Circle
Chapter 12	Surface Areas and Volumes
Chapter 13	Statistics
Chapter 14	Probability

Conclusion

If you want to improve your understanding of the concepts in the Triangle chapter, you can visit oswal.io. They offer a comprehensive collection of questions designed to help you practice and reinforce what you’ve learned. By engaging with these questions, you can strengthen your knowledge of triangles and become more proficient at solving problems related to this fundamental geometric shape.

Frequently Asked Questions

Q1. What is the Side-Side-Side (SSS) Similarity Criterion for triangles?

Ans: The Side-Side-Side (SSS) Similarity Criterion states that if the corresponding sides of any two triangles are in the same ratio, then their corresponding angles will be equal, and the triangles will be considered similar triangles.

Q2. What does the Basic Proportionality Theorem state?

Ans: The Basic Proportionality Theorem states that if a line is drawn parallel to one side of a triangle, intersecting the other two sides at distinct points, then the segments formed on those sides are divided in the same ratio. In other words, if we have a triangle ABC with a line PQ parallel to BC, intersecting AB at P and AC at Q, then the theorem asserts that AP/PB = AQ/QC.

Q.3 What are the six main types of triangles in mathematics, and how are they defined?

Ans: The six main types of triangles in mathematics are: ‍

Scalene Triangle: A scalene triangle has all three sides of different lengths, and all three angles are also different
Isosceles Triangle: An isosceles triangle has two sides of equal length, and consequently, two angles are also equal.
Equilateral Triangle: An equilateral triangle has all three sides of equal length, making all three angles equal to 60 degrees.
Acute Triangle: An acute triangle has all three angles less than 90 degrees.
Obtuse Triangle: An obtuse triangle has one angle that is greater than 90 degrees.
Right Triangle: A right triangle has one angle precisely equal to 90 degrees.

Q4. Explain the concept of congruence in triangles.

Ans: Congruence in triangles refers to the condition where two triangles have the same shape and size, and all their corresponding angles and sides are equal. When two triangles are congruent, they can be superimposed on each other, and their corresponding parts will coincide perfectly. This concept is denoted by the symbol “≅” and is used to establish the equality of triangles in various geometric proofs and constructions.

Q5. State the Pythagorean Theorem.

Ans: The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

Chapter Wise Important Questions for CBSE Board Class 10 Maths
Real Numbers
Polynomials
Pair of Linear Equations in Two Variables
Quadratic Equations
Arithmetic Progressions
Triangles
Coordinate Geometry
Introduction to Trigonometry
Some Applications of Trigonometry
Circles
Areas Related to Circles
Surface Areas and Volumes
Statistics
Probability

Class 10 Math Chapter 6 Triangles Important Questions

Introduction

What are Triangle?

Class 10 Triangles Important Questions and Answers

Q1. In ΔPQR, if PS is the internal bisector of ∠P meeting QR at S and PQ = 15 cm, QS = (3 + x) cm, SR = (x – 3) cm and PR = 7 cm, then find the value of x.

Options

(a) 2.85 cm (b) 8.25 cm (c) 5.28 cm (d) 8.52 cm

Q2. In the figure given below, ABC is a triangle. BC is parallel to AE. If BC = AC, then what is the value of ∠CAE?

Options

(a) 20° (b) 30° (c) 40° (d) 50°

Q3. D and E are points on sides AB and AC of triangle ABC such that DE || BC. If AD = 2·4 cm, DB = 3·6 cm and AC = 5 cm, find AE.

Q4. Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC at L and AD produced at E and AD = DE. Prove that EL = 2BL.

Q5. In ΔABC, AD is the bisector of ∠A. If AB = 5.6 cm, BD = 3.2 cm and BC = 6 cm, find AC.

CBSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. What is the Side-Side-Side (SSS) Similarity Criterion for triangles?

Q2. What does the Basic Proportionality Theorem state?

Q.3 What are the six main types of triangles in mathematics, and how are they defined?

Q4. Explain the concept of congruence in triangles.

Q5. State the Pythagorean Theorem.

Contact Us

Class 10 Math Chapter 6
Triangles
Important Questions

(a) 2.85 cm
(b) 8.25 cm
(c) 5.28 cm
(d) 8.52 cm

(a) 20°
(b) 30°
(c) 40°
(d) 50°