Polynomials

Home / Boards / CBSE / Important Questions / Class 10 / Maths / Polynomials

Class 10 Math Chapter 2
Polynomials
Important Questions

Q: Q1. Differentiate between monomial, binomial, trinomial, and multinomial.

Ans: Monomial: A polynomial with only one term, such as 5x^3, 2y, etc. Binomial: A polynomial with two terms, such as 3x + 2, 2y^2 – 5, etc. Trinomial: A polynomial with three terms, such as 4x^2 + 3x + 1, 2y^3 – 6y^2 + 7y, etc. Multinomial: A polynomial with more than three terms, such as 5x^4 + 2x^3 – 3x^2 + 7x – 1, etc

Here are some essential Class 10 Mathematics questions for Chapter 2, Polynomials. These carefully curated questions aim to assist students in their preparation for the CBSE Class 10 Mathematics Examination 2024-25. Practicing a diverse range of question types will not only help students clarify their doubts but also enable them to prepare more effectively for the exams. By solving these questions, students can build confidence in their problem-solving skills and enhance their overall performance in the Polynomials chapter.

Table of Contents

Introduction

In Chapter 2 of Class 10 Mathematics, Polynomials you will learn about polynomials, their types, and the concept of degree. Additionally, we will study the zeros of a polynomial and the relationship between zeros and coefficients of quadratic polynomials.

What are Polynomials?

A polynomial is a mathematical expression made up of variables (usually represented by the letters x, y, etc.), coefficients (real numbers), and non-negative integer exponents. The general form of a polynomial is given by:

P(x) = a_nx_n + a_(n-1)x_(n-1)+a_(n-2)x_(n-2) + \dots\dots\dots\dots\dots\dots. + a_1x + a_0

Where

a_n, a_(n-1), a_(n-2), \dots\dots\dots\dots\dots\dots\dots\dots, a_1, a_0

are called coefficients of

x_n, x_(n-1), x_(n-2), \dots.., x

and constant term respectively and it should belong to a real number.

Class 10 Polynomials Important Questions and Answers

Q 1. If one of the quadratic polynomial $x^2 + 3x + k$ is 2, then the value of k is:

Options

(a) 10
(b) -10
(c) -7
(d) -2

Ans. (b)

Explanation:
Let    p(x) = $x^2$ + 3x + k
∵          x = 2 is a zero of p(x)
∴    p(2) = 0
⇒ $(2)^2$ + 3(2) + k = 0
⇒ 4 + 6 + k = 0
⇒ 10 + k = 0
⇒ k = -10

Q 2. Write the zeros of the polynomial.

$f(x) = x^2 - x - 6$

options

(a) -3,2
(b) -3 -2
(c) 3, 2
(d) 3, -2

Ans. (d)

Explanation:
$f(x) = x^2 + x - 6 \\ \space\space\space\space\space\space\space = x^2 - 3x + 2x - 6$

         = x(x - 3) + 2(x - 3)
         = (x + 2)(x - 3)
To find zeros put f(x) = 0
∴           x = -2, 3

Q 3. Solve for x:

$3x^2 - 2\sqrt{6x}+2 = 0$

Explanation:
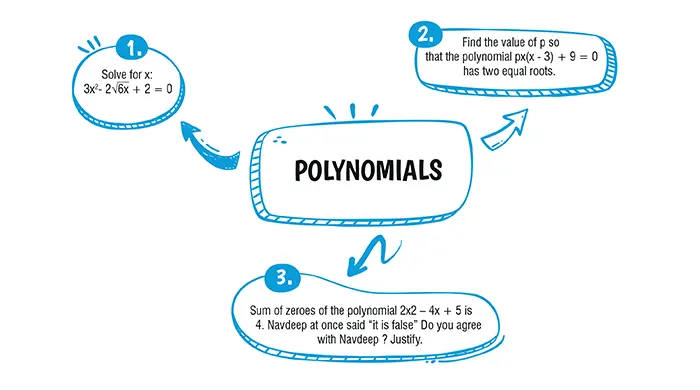
Given, $3x^2 – 2\sqrt{6x} + 2 = 0 \\ [4 bp] \Longrightarrow 3x^2 – \sqrt{6x} – \sqrt{6x} + 2 = 0 \\ [4 bp] \Longrightarrow \sqrt{3x}(\sqrt{3x} – \sqrt{2}) – \sqrt{2}(\sqrt{3x} – \sqrt{2}) = 0 \\ [4 bp] \Longrightarrow (\sqrt{3x} – \sqrt{2}) – (\sqrt{3x} – \sqrt{2}) = 0 \\ [4 bp] \Longrightarrow x = \sqrt{\frac{2}{3}}, \sqrt{\frac{2}{3}}$

Q 4. Find the value of p so that the polynomial px(x - 3) + 9 = 0 has two equal roots.

Explanation:
Given,
$px(x - 3) + 9 = 0 \\ [4 bp] \text{or} \space\space\space\space px^2 - 3px + 9 = 0 \\ [4 bp]$ Let ⍺, β be the zeroes of the polynomial.
Then, $\alpha + \beta$ = 3 and $\alpha \beta = \frac{9}{p} \\ [4 bp] \text{Also,} \alpha = \beta \\ [4 bp] \therefore 2\alpha = 3 \\ [4 bp] \text{or} \alpha = \beta = \frac{3}{2} \\ [4 bp] \therefore \frac{9}{4} = \frac{9}{p} \\ [4 bp] \Longrightarrow p = 4 \\ [4 bp]$

Hence, the zeroes of the polynomial px(x - 3) + 9 = 0 will be equal when p = 4.

Q 5. Sum of zeroes of the polynomial $2x^2$ – 4x + 5 is 4. Navdeep at once said “it is false” Do you agree with Navdeep ? Justify.

Explanation:
Yes
On comparing the given equation with $ax^2$ + bx + c,
We get
Here a = 2, b = -4, c = 5

\text{Sum of zeroes = }\dfrac{–b}{a}=\dfrac{–(–4)}{2} = \dfrac{4}{2} = 2 \\ [4 bp] \therefore \text{ Navdeep is right.}

If you are looking to further practice and enhance your understanding of the concepts discussed in the chapter, oswal.io provides a comprehensive set of questions for understanding the concept in a better way.

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now

CBSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Real Numbers
Chapter 2	Polynomials
Chapter 3	Pair of Linear Equations in Two Variable
Chapter 4	Quadratic Equations
Chapter 5	Arithmetic Progressions
Chapter 6	Triangles
Chapter 7	Coordinate Geometry
Chapter 8	Introduction to Trigonometry
Chapter 9	Some Applications of Trigonometry
Chapter 10	Circles
Chapter 11	Areas Related to Circle
Chapter 12	Surface Areas and Volumes
Chapter 13	Statistics
Chapter 14	Probability

Conclusion

The chapter on Polynomials helps students develop algebraic skills and prepares them for more advanced topics in higher classes. It also finds practical applications in various fields such as science, engineering, and economics. Understanding polynomials is crucial for building a strong foundation in algebra and problem-solving skills.

Frequently Asked Questions

Q1. Differentiate between monomial, binomial, trinomial, and multinomial.

Ans: Monomial: A polynomial with only one term, such as

5x^3, 2y,

etc. Binomial: A polynomial with two terms, such as 3x + 2,

2y^2 - 5,

etc. Trinomial: A polynomial with three terms, such as

4x^2 + 3x + 1, 2y^3 - 6y^2 + 7y,

etc. Multinomial: A polynomial with more than three terms, such as

5x^4 + 2x^3 - 3x^2 + 7x - 1,

etc

Q2. How do you find the degree of a polynomial? Explain with examples.

Ans: The degree of a polynomial is the highest power of the variable ‘x’ (or any other variable) in the expression. To find the degree, identify the term with the highest power of the variable.

Q3. What is the Factor Theorem? How is it useful in finding factors and roots of polynomials?

Ans: Factor Theorem: If P(a) = 0, then (x – a) is a factor of the polynomial P(x). The Factor Theorem helps in finding factors and roots of polynomials. If we know one root (zero) of a polynomial, we can easily find the corresponding factor. Additionally, it simplifies the process of polynomial factorization.

Q4. State the degree of the zero polynomial.

Ans: The degree of the zero polynomial is undefined since it does not have any terms.

Q5. If the degree of a polynomial is 'n,' what is the maximum number of roots it can have?

Ans: The maximum number of roots a polynomial of degree ‘n’ can have is ‘n’.

Chapter Wise Important Questions for CBSE Board Class 10 Maths
Real Numbers
Polynomials
Pair of Linear Equations in Two Variables
Quadratic Equations
Arithmetic Progressions
Triangles
Coordinate Geometry
Introduction to Trigonometry
Some Applications of Trigonometry
Circles
Areas Related to Circles
Surface Areas and Volumes
Statistics
Probability

Class 10 Math Chapter 2 Polynomials Important Questions