Table of Contents
Ans.(b) 14
Explanation:
Surface area of sphere = 616 cm^2\\
⇒ 4πr^2 = 616\\
⇒ 4 × \dfrac{22}{7}× r^2 = 616\\
⇒ r^2 = 616 × \dfrac{7}{22×4}\\
⇒ r = 7 cm\\
So, the diameter = 2r = 2 × 7 = 14 cm.
Ans. (b) 1:64
Explanation:
The diameter of Moon is approximately one fourth of the diameter of Earth.
Let, Radius of Moon = r,
Then, Radius of Earth = 4r
\text{Required ratio = }\dfrac{\text{Volume of Moon}}{\text{Volume of Earth}} \\= \dfrac{\dfrac{4}{3}\pi r^3}{\dfrac{4}{3}\pi (4r)^3}\\= \dfrac{r^3}{64r^3} = \dfrac{1}{64}\\
= 1:64
Explanation:
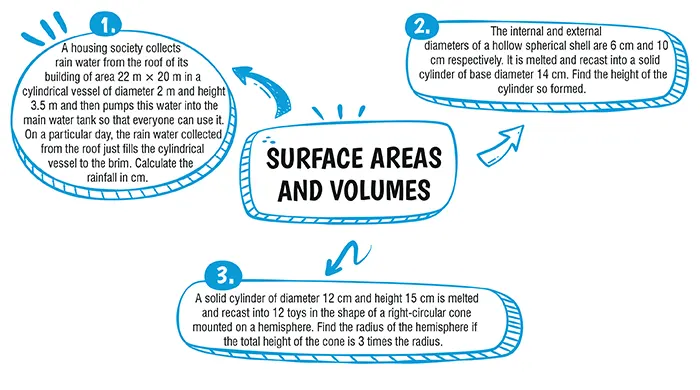
Given, Area of the roof = 22 m × 20 cm
Height of cylindrical vessel = 3.5 m
Diameter of the vessel = 2 m
∴ Radius of the vessel = 1 m
Let the total rainfall be h m.
∴ Volume of rain water collected on the roof
= volume of the cylindrical vessel
\\
⇒ 22 × 20 × h = π (1)^2 (3.5)\\[4.5 bp]
⇒ 22 × 20 × h = \dfrac{22}{7} (3.5)\\[4.5 bp]
⇒ 20 h = 0.5 \\[4.5 bp]
⇒ h = \dfrac{1}{40}m = 2.5 cm.
Explanation:
Given, internal diameter of sphere = 6 cm
External diameter of sphere = 10cm
Base diameter of cylinder = 14 cm
Thus, internal radius of sphere ,r_1 = 3 cm\\
External radius of sphere r_2 = 5 cm\\
Base radius of cylinder, r = 7 cm
Let the height of the cylinder be h cm.
Thus, volume of cylinder = Volume of spherical shell
πr^2h = \dfrac{4}{3}π(r_2^3 -r_1^3) \\
⇒ π(7)^2h = \dfrac{4}{3}π[(5)^3 - (3)^3]\\[4.5 bp]
⇒ 3(7)^2h = 4 [(5)^3 - (3)^3]\\[4.5 bp]
⇒ 3(49)h = 4 [125 - 27]\\[4.5 bp]
⇒ 3(49)h = 4 [98]\\[4.5 bp]
⇒ 3h = 4 [2]\\[4.5 bp]
⇒ h = \dfrac{8}{3} cm. \\[4.5 bp]
Explanation:
Ans. Given, Diameter of the cylinder = 12 cm
∴ Radius = 6 cm
Height of the cylinder = 15 cm
Number of toys = 12
Let the radius of the hemisphere be r cm
Thus, height of the cone = 3r cm
Now, volume of cylinder = π(6)^2 15 cm^3\\=\text{ (36) (15) π cm}^3 \\\text{= 540 π cm}^3\\Now, total volume of 12 toys
= 12 [volume of hemisphere + volume of cone]
Thus, total volume of 12 toys
= 12\bigg[\dfrac{1}{3} \pi (3r)(r)^2 + \dfrac{2}{3} \pi r^3\bigg] cm^3 \\[4.5 bp]= 4[3πr^3 + 2πr^3]cm^3\\[4.5 bp]=20πr^3 cm^3\\[4.5 bp]Now, 20πr^3 = 540π\\[4.5 bp]⇒ r^3 = 27 \\[4.5 bp]⇒ r^3 = (3)^3\\[4.5 bp]⇒ r = 3 cm
Thus, radius of the hemisphere = 3 cm and height of the cone = (3)(3) cm =9 cm
∴ Total height of the toy
= (9 + 3) cm = 12 cm.
| Chapter No. | Chapter Name |
|---|---|
| Chapter 1 | Real Numbers |
| Chapter 2 | Polynomials |
| Chapter 3 | Pair of Linear Equations in Two Variable |
| Chapter 4 | Quadratic Equations |
| Chapter 5 | Arithmetic Progressions |
| Chapter 6 | Triangles |
| Chapter 7 | Coordinate Geometry |
| Chapter 8 | Introduction to Trigonometry |
| Chapter 9 | Some Applications of Trigonometry |
| Chapter 10 | Circles |
| Chapter 11 | Areas Related to Circle |
| Chapter 12 | Surface Areas and Volumes |
| Chapter 13 | Statistics |
| Chapter 14 | Probability |
| Chapter Wise Important Questions for CBSE Board Class 10 Maths |
|---|
| Real Numbers |
| Polynomials |
| Pair of Linear Equations in Two Variables |
| Quadratic Equations |
| Arithmetic Progressions |
| Triangles |
| Coordinate Geometry |
| Introduction to Trigonometry |
| Some Applications of Trigonometry |
| Circles |
| Areas Related to Circles |
| Surface Areas and Volumes |
| Statistics |
| Probability |
CBSE Important Questions Class 9
CBSE Important Questions Class 10
CBSE Important Questions Class 12
CBSE Practice Papers
CBSE Practice Papers
ICSE Important Questions Class 9
ICSE Important Questions Class 10
ICSE Practice Papers
ISC Important Questions Class 12
ISC Practice Papers
Contact Us
CBSE
Important Questions
Class 10
Maths
Science
Social Science
English
Chemistry
Biology
Physics
Computer Applications
History & Civics
Geography
Business Studies
Economics
Accountancy
Political Science
General Test
