Table of Contents
Ans.(c) \dfrac{12}{13}
Explanation:
Total number of possible outcomes = 52
Number of aces in the pack = 4
Thus, the probability of not drawing an ace
\therefore P(E) = \dfrac{52-4}{52} = \dfrac{48}{52} = \dfrac{12}{13}
Ans. (b) \dfrac{3}{5}
Explanation:
Total number of possible outcomes = 10
The total number of favourable outcomes = 6
\therefore P(E) = \dfrac{6}{10} = \dfrac{3}{5}
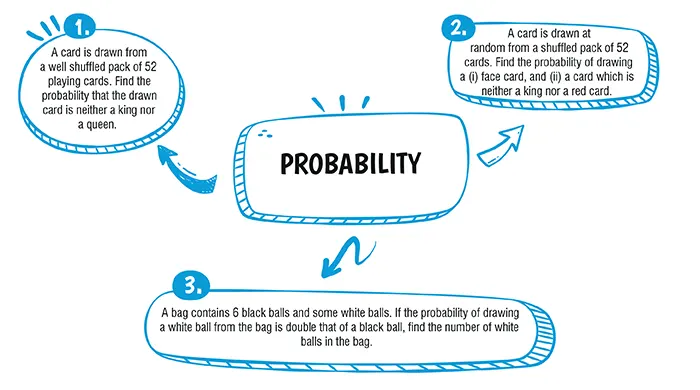
Explanation:
The number of cards =52
Number of kings and queens=4+4=8
Thus, number of favourable outcomes
= 52−8 = 44
\therefore P(E) = \dfrac{44}{52} = \dfrac{11}{13}
Explanation:
Total numbers of cards = 52
(i) The number of favourable outcomes of drawing a face card = 12
\\ \therefore P(E) = \dfrac{12}{52} = \dfrac{3}{13}\\
(ii) The number of favourable outcomes of drawing neither a king nor a red card
= 52 – (2 + 26)
= 24
\therefore P(E) = \dfrac{24}{52} = \dfrac{6}{13}\\
Explanation:
Let the number of white balls be x.
Thus, the total number of the possible outcomes
= 6 + x
Now, the favourable outcomes if the black ball is drawn = 6
\therefore P(B) = \dfrac{6}{6+x}\\
Again, the favourable outcomes if the white ball is drawn = x
\therefore P(W) = \dfrac{6}{6+x}\\
According to the question,
\dfrac{6}{6+x} = 2\left(\dfrac{6}{6+x}\right)\\
⇒ x = 12
Hence, the number of white balls = 12.
| Chapter No. | Chapter Name |
|---|---|
| Chapter 1 | Real Numbers |
| Chapter 2 | Polynomials |
| Chapter 3 | Pair of Linear Equations in Two Variable |
| Chapter 4 | Quadratic Equations |
| Chapter 5 | Arithmetic Progressions |
| Chapter 6 | Triangles |
| Chapter 7 | Coordinate Geometry |
| Chapter 8 | Introduction to Trigonometry |
| Chapter 9 | Some Applications of Trigonometry |
| Chapter 10 | Circles |
| Chapter 11 | Areas Related to Circle |
| Chapter 12 | Surface Areas and Volumes |
| Chapter 13 | Statistics |
| Chapter 14 | Probability |
| Chapter Wise Important Questions for CBSE Board Class 10 Maths |
|---|
| Real Numbers |
| Polynomials |
| Pair of Linear Equations in Two Variables |
| Quadratic Equations |
| Arithmetic Progressions |
| Triangles |
| Coordinate Geometry |
| Introduction to Trigonometry |
| Some Applications of Trigonometry |
| Circles |
| Areas Related to Circles |
| Surface Areas and Volumes |
| Statistics |
| Probability |
CBSE Important Questions Class 10
ICSE Important Questions Class 10
CBSE Important Questions Class 10
ICSE Important Questions Class 10
CBSE
Important Questions
Class 10
Maths
Science
Social Science
English
Biology
Physics
Chemistry
Computer Applications
History & Civics
Geography
Business Studies
Economics
Accountancy
Political Science
General Test
