Pair of Linear Equations in Two Variables

Home / Boards / CBSE / Important Questions / Class 10 / Maths / Pair of Linear Equations in Two Variables

Class 10 Maths Chapter 3
Pair of Linear Equation in Two Variables
Important Questions

Here are some important Class 10 Mathematics questions for Chapter 3, Pair of Linear Equations in Two Variables. These thoughtfully selected questions are designed to support students in their preparation for the CBSE Class 10 Mathematics Examination 2024-25. Practicing various question types will not only clarify doubts but also improve exam readiness. By solving these questions, students can boost their confidence in problem-solving and excel in the Pair of Linear Equations in Two Variables chapter.

Table of Contents

Introduction

In Chapter 3, “Pair of Linear Equations in Two Variables,” we explore the graphical method of solving a system of two linear equations. The concept involves representing both equations graphically on the Cartesian plane and finding the point of intersection, which corresponds to the solution of the equations.

What are pair of linear equations in two Variables?

A pair of linear equations in two variables is a set of two equations of the form: ax + by = c px + qy = r where ‘x’ and ‘y’ are the variables, and ‘a’, ‘b’, ‘p’, ‘q’, ‘c’, and ‘r’ are constants with at least one of ‘a’ and ‘ B ‘ or ‘p’ and ‘q’ is not equal to zero.

Class 10 Pair of Linear Equations in Two Variables Important Questions and Answers

Q 1. If 2x - 3y = 7 and (a + b) x - (a + b - 3)y = 40 represent______ lines, then a and b satisfy the equation a - 5b = 0.

Options

(a) Coincident
(b) Parallel
(c) Unique
(d) None of these

Ans. (a)

Explanation:
$\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} \\[4 bp] \frac{2}{a+b} = \frac{3}{a+b–3} \\ [4 bp] \space\space\space\space\space\space= \frac{7}{4a+b} \\ [4 bp] \frac{2}{a+b} = \frac{7}{4a+b}\\[4 bp]$

8a + 2b = 7a + 7b
a – 5b = 0
Hence lines are coincident.

Q 2. The pair equations y = 0 and y = - 7 has:

Options

(a) One solution
(b) Two solution
(c) Infinitely many solutions
(d) No solution

Ans. (d)

Explanation:
The given pair of equations y = 0 and y = - 7

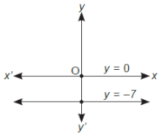
By graphically both lines are parallel and have no solution.

Q 3. Cost of 2 pens and 3 pencils together is ₹ 40 and the cost of 6 pens and 9 pencils together is ₹ 130. Express above statement in the form of linear equations.

Explanation:
Let the cost of 1 pen be ₹ x and cost of 1 pencil be ₹ y
Then,
2x + 3y = 40
and 6x + 9y =130

Q 4. Find whether the following system of equations is consistent or inconsistent :

${\Large\frac{3}{2}}x+{\Large\frac{5}{3}}y = 7 \text{ and 9x - 10y = 14.}$

Explanation:
‍We have,
$\space\space\space\space\space\space\space\space\space\space\space\space {\Large\frac{3}{2}}x+{\Large\frac{5}{3}}y - 7 = 0 \\[4.5bp] and \space\space\space\space 9x - 10y - 14 = 0 \\[4.5bp]$ $\text{Here,} \space\space\space\space a_1 = \frac{3}{2}, \space b_1 = \frac{5}{3}, c_1 = -7, \\[4.5bp] \space\space\space\space\space\space\space\space\space\space\space\space\space\space a_2 = 9, b_2 = - 10, c_2 = - 14 \\[4.5bp]$ $\text{Thus, } \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space {\Large\frac{a_1}{a_2}}={\Large \frac{3}{2×9}} = {\Large\frac{1}{6}}, {\Large\frac{b_1}{b_2}}={\Large\frac{3}{3(-10)}}=-{\Large\frac{1}{10}}\\[4.5bp]$ $\text{Since, }\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space {\Large\frac{a_1}{a_2}}\not= {\Large\frac{b_1}{b_2}}$

So, given system of equations has unique and it is consistent.

Q 5. Given the linear equation x – 2y – 6 = 0, write another linear equation in these two variables, such that the geometrical representation of the pair so formed is:

(i) coincident lines
(ii) intersecting lines

Explanation:
(i) Given, x - 2y - 6 = 0

For lines to be coincident, the condition is:

\space\space\space\space\space\space\space\space\space {\Large\frac{a_1}{a_2}}={\Large\frac{b_1}{b_2}}={\Large\frac{c_1}{c_2}} \\[4.5 bp]

Thus, one possible option can be:
$\space\space\space\space\space\space\space\space\space 2x - 4y - 12 = 0 \\ [4.5 bp] \text{Here,} \space\space\space\space\space\space\space\space\space\space a_1 = 1, b_1 = - 2, c_1 = - 6. \\ [4.5 bp] \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space a_2 = 2, b_2 = - 4, c_2 = - 12. \\ [4.5 bp] {\Large\frac{a_1}{a_2}} = {\Large\frac{1}{2}};{\Large\frac{b_1}{b_2}}= {\Large\frac{-2}{-4}}={\Large\frac{1}{2}}; {\Large\frac{c_1}{c_2}}={\Large\frac{-6}{-12}}={\Large\frac{1}{2}}\\[4.5bp]$ $∴ \space\space\space\space\space\space\space\space\space {\Large\frac{a_1}{a_2}}={\Large\frac{b_1}{b_2}}={\Large\frac{c_1}{c_2}}\\[4.5 bp]$

So, it shows coincident lines.‍

(ii) Given, 2x - 2y - 6 =0
For intersecting lines

\space\space\space\space\space\space\space\space\space\space {\Large\frac{a_1}{a_2}}\not={\Large\frac{b_1}{b_2}} \\ [4.5 bp]

Thus, one possible can be:
2x - 7y - 13 = 0
Here,

\space\space\space\space\space\space\space\space\space\space a_1 = 1, \space b_1 = - 2, \space c_1 = - 6. \\ [4.5 bp] \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space a_2 = 2, \space b_2 = - 7, \space c_2 = - 13.\\ [4.5bp] {\Large\frac{a_1}{a_2}}= {\Large\frac{1}{2}}, {\Large\frac{b_1}{b_2}} = {\Large\frac{-2}{-7}}={\Large\frac{2}{7}}\\[4.5bp]

∴ \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space{\Large\frac{a_1}{a_2}} ≠ {\Large\frac{b_1}{b_2}} \\[4.5bp]

So, they represent intersecting lines.

If you are looking to further practice and enhance your understanding of the concepts discussed in the chapter, oswal.io provides a comprehensive set of questions for understanding the concept in a better way.

CBSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Real Numbers
Chapter 2	Polynomials
Chapter 3	Pair of Linear Equations in Two Variable
Chapter 4	Quadratic Equations
Chapter 5	Arithmetic Progressions
Chapter 6	Triangles
Chapter 7	Coordinate Geometry
Chapter 8	Introduction to Trigonometry
Chapter 9	Some Applications of Trigonometry
Chapter 10	Circles
Chapter 11	Areas Related to Circle
Chapter 12	Surface Areas and Volumes
Chapter 13	Statistics
Chapter 14	Probability

Conclusion

If you are seeking additional practice and a deeper grasp of the concepts covered in the chapter, oswal.io offers a wide-ranging collection of questions that will help you gain a more comprehensive understanding of the topic. By exploring their extensive question bank, you can reinforce your knowledge, improve your problem-solving abilities.

Frequently Asked Questions

Q1. What are the algebraic methods to solve a pair of linear equations in two variables?

Ans: The two common algebraic methods are the substitution method and the elimination method.

Q2. How are pairs of linear equations in two variables solved graphically?

Ans: Graphical method involves plotting both equations on a Cartesian plane as lines and finding the point of intersection, which represents the solution to the system.

Q3. Can a pair of linear equations have more than one solution?

Ans: Yes, if the two lines representing the equations coincide (overlap), the system has infinitely many solutions.

Q4. What is the graphical method of solving a pair of linear equations?

Ans: The graphical method involves representing each equation on the Cartesian plane as a straight line by plotting its intercepts or using the slope-intercept form. The solution to the pair of equations is the point of intersection of these lines on the graph.

Q5. Is it possible for a pair of linear equations to have no solution?

Ans: Yes, if the two lines representing the equations are parallel and do not intersect, the system has no solution.

Chapter Wise Important Questions for CBSE Board Class 10 Maths
Real Numbers
Polynomials
Pair of Linear Equations in Two Variables
Quadratic Equations
Arithmetic Progressions
Triangles
Coordinate Geometry
Introduction to Trigonometry
Some Applications of Trigonometry
Circles
Areas Related to Circles
Surface Areas and Volumes
Statistics
Probability

Class 10 Maths Chapter 3 Pair of Linear Equation in Two Variables Important Questions

Introduction

What are pair of linear equations in two Variables?

Class 10 Pair of Linear Equations in Two Variables Important Questions and Answers

Q 1. If 2x - 3y = 7 and (a + b) x - (a + b - 3)y = 40 represent______ lines, then a and b satisfy the equation a - 5b = 0.

Options

(a) Coincident(b) Parallel(c) Unique(d) None of these

Q 2. The pair equations y = 0 and y = - 7 has:

Options

(a) One solution(b) Two solution(c) Infinitely many solutions(d) No solution

Q 3. Cost of 2 pens and 3 pencils together is ₹ 40 and the cost of 6 pens and 9 pencils together is ₹ 130. Express above statement in the form of linear equations.

Q 4. Find whether the following system of equations is consistent or inconsistent :

{\Large\frac{3}{2}}x+{\Large\frac{5}{3}}y = 7 \text{ and 9x - 10y = 14.}

Q 5. Given the linear equation x – 2y – 6 = 0, write another linear equation in these two variables, such that the geometrical representation of the pair so formed is:

(i) coincident lines(ii) intersecting lines

CBSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. What are the algebraic methods to solve a pair of linear equations in two variables?

Q2. How are pairs of linear equations in two variables solved graphically?

Q3. Can a pair of linear equations have more than one solution?

Q4. What is the graphical method of solving a pair of linear equations?

Q5. Is it possible for a pair of linear equations to have no solution?

Class 10 Maths Chapter 3
Pair of Linear Equation in Two Variables
Important Questions

(a) Coincident
(b) Parallel
(c) Unique
(d) None of these

(a) One solution
(b) Two solution
(c) Infinitely many solutions
(d) No solution

${\Large\frac{3}{2}}x+{\Large\frac{5}{3}}y = 7 \text{ and 9x - 10y = 14.}$

(i) coincident lines
(ii) intersecting lines