Table of Contents
Explanation:
\space\space\space\space\space\space \cos^4 θ - \sin^4 θ = \dfrac{2}{3} \\[4.5 bp]
⇒ \space\space\space\space\space\space (\cos^2 θ)^2 - (\sin^2 θ)^2 = \dfrac{2}{3} \\[4.5 bp]
⇒\space\space\space\space\space\space (\cos^2 θ + \sin^2 θ)(\cos^2 θ - \sin^2 θ) = \dfrac{2}{3} \\[4.5 bp]
⇒\space\space\space\space\space\space \cos^2 θ - \sin^2 θ = \dfrac{2}{3} \\[4.5 bp] \space\space\space\space\space\space(∵ \sin^2 θ + \cos^2 θ = 1) \\[4.5 bp]
⇒\space\space\space\space\space\space 1- \sin^2 θ - \sin^2 θ = \dfrac{2}{3} \\[4.5 bp]\space\space\space\space\space\space(∵ \cos^2 θ = 1- \sin^2 θ) \\[4.5 bp]
⇒\space\space\space\space\space\space 1 - 2 \sin^2 θ =\dfrac{2}{3}
Explanation:
Given : \tan \space A =\dfrac{1}{\sqrt{5}} \\[4.5 bp]
\Rightarrow \space\space\space\space \tan^2{A}=\dfrac{1}{5} \space\space\space\space ...(i) \\[4.5 bp]
\Rightarrow \space\space\space\space
\dfrac{1}{\cot^2A}=\dfrac{1}{5} \\[4.5 bp] \space\space\space\space
\begin{bmatrix}
∵ \space\space\space\space \tan A = \dfrac{1}{\cot A}\end{bmatrix} \\[4.5 bp]
⇒\space\space\space\space \cot^2 A = 5 \space\space\space\space …(ii) \\[5 bp]
\text{Now,} \space \space \dfrac{\cosec^2A - \sec^2A}{\cosec^2A + \sec^2A}=\dfrac{1+\cot^2A-(1+\tan^2A)}{1 + \cot^2A+1 + \tan^2A} \\[4.5 bp]
[∵ \cosec^2 A = 1 + \cot^2 A \space \\
and \space sec^2 A = 1 + \tan^2 A ] \\[5 bp]
=\space\space\space\space
\dfrac{\cot^2A-\tan^2A}{2 + \cot^2A + \tan^2A}=\dfrac{5-\dfrac{1}{5}}{2+5+\dfrac{1}{5}} \\[4.5 bp]
\left[\text{ From (i) and (ii) }\right] \\[4.5 bp]
= \space\space\space\space \dfrac{\dfrac{25-1}{5}}{\dfrac{35+1}{5}}=\dfrac{24}{36} = \dfrac{2}{3} \\[5 bp]
\dfrac{\cosec^2A-\sec^2 A}{\cosec^2A+sec^2 A}=\dfrac{2}{3}
Explanation:
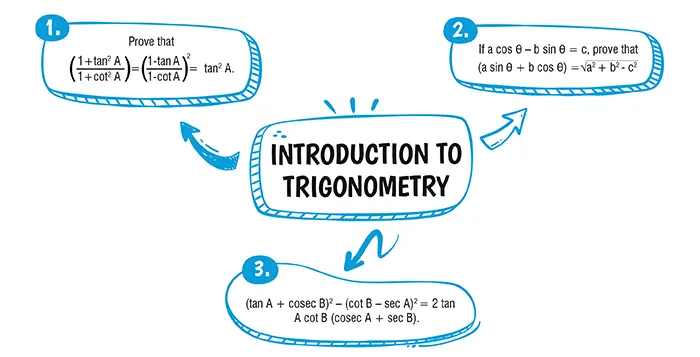
\text{Given, a cos θ – b sin θ = c ...(i)} \\[4.5 bp]
\text{Now, }a^2 + b^2 – c^2 = a^2 + b^2 – (a \cos θ – b \sin θ)^2 \text{\space \space \space \space [From (i)]}\\[4.5 bp]
= a^2 + b^2 – (a^2 cos^2 θ + b^2 \sin^2 θ – 2ab \sin θ cos θ) \\[4.5 bp]
= a^2 + b^2 – [a^2(1 – \sin^2 θ) + b^2(1 – \cos^2 θ) – 2ab \sin θ \cos θ]\\[4.5 bp]
= a^2 + b^2 – [a^2 – a^2 \sin^2 θ + b^2 – b^2 \cos^2 θ – 2ab \sin θ \cos θ]\\[4.5 bp]
= a^2 + b^2 – a^2+ a^2 \sin^2 θ – b^2 + b^2 \cos^2 θ + 2ab \sin θ \cos θ]\\[4.5 bp]
= a^2sin^2 θ + b^2 \cos^2 θ + 2ab \sin θ \cos θ \\[4.5 bp]
= (a \sin θ + b \cos θ)^2\\[4.5 bp]
\text{Thus, }a^2 + b^2 – c^2 = (a \sin θ + b \cos θ)^2\\[4.5 bp]
\text{or }\space \space \space \sqrt{a^2 + b^2 - c^2} = (a\space \sin \spaceθ + b\space \cos \spaceθ)\\[4.5 bp]
\rArr \space \space \space
(a\space \sin \spaceθ + b\space \cos \spaceθ) = \sqrt{a^2 + b^2 - c^2}.
Ans. L.H.S. = R.H.S.
Explanation:
L.H.S. = (\tan\space A + \cosec\space B)^2 – (\cot\space B – \sec\space A)^2 \\[5.5 bp]
= \tan^2 A + \cosec^2 B + 2 \tan A. \cosec\space B – (\cot^2\space B + \sec^2\space A – 2 \cot \space B. \sec\space A) \\[5.5 bp]
= \tan^2\space A + \cosec^2 B + 2 \tan \space A. \cosec\space B – \cot^2\space B – \sec^2\space A + 2 \cot\space B \sec\space A \\[5.5 bp]
= (\cosec^2\space B – \cot^2\space B) – (\sec^2\space A – \tan^2 A) + 2 \tan\space A.\cosec \space B + 2 \cot \space B \sec \space A \\[5.5 bp]
= 1 – 1 + 2 \tan \space A. \cosec \space B + 2 \cot \space B. \sec \space A \\[5.5 bp]
= 2 \tan \space A. \cosec \space B + 2 \cot \space B.\sec \space A \\[5.5 bp]
=2\begin{pmatrix} \dfrac {\sin \space A}{\cos \space A}×\dfrac{1}{\sin B}+\dfrac{\cos \space B}{\sin B}×\dfrac{1}{\cos \space A}\end{pmatrix} \\[5.5 bp]
=2\begin{pmatrix} \dfrac{\sin \space A + \cos \space B}{\cos \space A. \sin \space B}\end{pmatrix}...(i) \\[5.5 bp]
R.H.S. = 2 tan A.cot B.(cosec A + sec B)
= 2 tan A.cot B. cosec A + 2 tan A. cot B.sec B
=2\dfrac{\sin \space A}{\cos\space A}.\dfrac{\cos\space B}{\sin\space A}.\dfrac{1}{\sin\space A}+\dfrac{2 \sin A}{\cos \space A}.\dfrac{\cos B}{\sin\space B}.\dfrac{1}{\cos\space B} \\[5.5 bp] =2\begin{pmatrix} \dfrac{\cos\space B}{\cos\space A.\sin\space B}+\dfrac{sin \space A}{\cos A. \sin B}\end{pmatrix} \\[5.5 bp] =2 \begin{pmatrix} \dfrac{\cos B+ \sin A}{\cos\space A. \sin\space B}\end{pmatrix}\text{ ....(ii)} \\[5.5 bp] \text{ From (i) and (ii), } \\[5.5 bp] \text{L.H.S. = R.H.S. }| Chapter No. | Chapter Name |
|---|---|
| Chapter 1 | Real Numbers |
| Chapter 2 | Polynomials |
| Chapter 3 | Pair of Linear Equations in Two Variable |
| Chapter 4 | Quadratic Equations |
| Chapter 5 | Arithmetic Progressions |
| Chapter 6 | Triangles |
| Chapter 7 | Coordinate Geometry |
| Chapter 8 | Introduction to Trigonometry |
| Chapter 9 | Some Applications of Trigonometry |
| Chapter 10 | Circles |
| Chapter 11 | Areas Related to Circle |
| Chapter 12 | Surface Areas and Volumes |
| Chapter 13 | Statistics |
| Chapter 14 | Probability |
| Chapter Wise Important Questions for CBSE Board Class 10 Maths |
|---|
| Real Numbers |
| Polynomials |
| Pair of Linear Equations in Two Variables |
| Quadratic Equations |
| Arithmetic Progressions |
| Triangles |
| Coordinate Geometry |
| Introduction to Trigonometry |
| Some Applications of Trigonometry |
| Circles |
| Areas Related to Circles |
| Surface Areas and Volumes |
| Statistics |
| Probability |
CBSE Important Questions Class 9
CBSE Important Questions Class 10
CBSE Important Questions Class 12
CBSE Practice Papers
CBSE Practice Papers
ICSE Important Questions Class 9
ICSE Important Questions Class 10
ICSE Practice Papers
ISC Important Questions Class 12
ISC Practice Papers
Contact Us
CBSE
Important Questions
Class 10
Maths
Science
Social Science
English
Chemistry
Biology
Physics
Computer Applications
History & Civics
Geography
Business Studies
Economics
Accountancy
Political Science
General Test
