Coordinate Geometry

Home / Boards / CBSE / Important Questions / Class 10 / Maths / Coordinate Geometry

Class 10 Math Chapter 7
Coordinate Geometry

Q: Q3: How do you find the distance between two points on the coordinate plane?

Ans: The distance between two points (x_1, y_1) and (x_2, y_2) on the coordinate plane can be calculated using the Distance Formula: Distance = √[(x₂ – x₁)² + (y₂ – y₁)²]

Here are some essential Class 10 Mathematics questions for Chapter 7, Coordinate Geometry , carefully selected to assist students in preparing for the CBSE Class 10 Mathematics Examination in 2024-25. These thoughtfully curated questions cover various types of problems and aim to help students strengthen their problem-solving skills and gain a deeper understanding of the Coordinate Geometry chapter. By practicing this diverse range of questions, students can clarify any doubts they may have and improve their performance in this chapter.

Table of Contents

Introduction

In this chapter, we will study concepts of coordinate geometry, graphs of linear equations, the distance formula, and the section formula for internal division.These concepts are essential in understanding the relationship between algebra and geometry.

What are Coordinate Geometry?

Coordinate Geometry is a branch of mathematics that deals with the study of geometrical figures using a coordinate system. It involves representing points, lines, and shapes on a plane using ordered pairs of numbers (x, y) called coordinates.

Class 10 Coordinate Geometry Important Questions and Answers

Q1. In the second quadrant, for a point, the abscissais ........... and the ordinate is ........... .

Options

(a) positive, negative
(b) negative, positive
(c) negative, negative
(d) positive, positive

Ans.(b)

Explanation:
In the second quadrant, X-axis is negative and Y-axis is positive. Therefore, for a point the
abscissa is negative and the ordinate is positive.

Q2. What is the ratio in which the line joining the points (6, 4) and (1, – 7) is divided by the X-axis?

Options

(a) 5 : 4
(b) 4 : 7
(c) 7 : 4
(d) 4 : 5

Ans. (b)

Explanation:
Let, k : 1 be the ratio in which the X-axis divides the line joining (6,4) and (1,-7).
Let, P be the point on the X- axis that divides the line.
$\text{Then} \space \space P(x,y)=\begin{pmatrix} \dfrac{k+6}{k+1},\dfrac{-7k+4}{k+1}\end{pmatrix} \\[4.5 bp] \text{As P(x,y) lies on X-axis } \space P(x,0)=\begin{pmatrix} \dfrac{k+6}{k+1},\dfrac{-7k+4}{k+1} \end{pmatrix} \\[4.5 bp] \text{[∵ x- coordinate will be (x,0)]} \\[4.5 bp] \Rightarrow \dfrac{-7k+4}{k+1}=0 \\[4.5 bp] ⇒ -7k+4 = 0 \\[4.5 bp] ⇒ 7k=4 \\[4.5 bp] \Rightarrow k= \dfrac{4}{7} \\[4.5 bp] \text{So, the required ratio be} \space \space k : 1 =\dfrac{4}{7}:1= 4 : 7$

Q3. Find the coordinates of point A, where AB is the diameter of a circle whose center is (2, – 3) and B is the point (1,4).

Explanation:
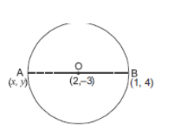
Let the coordinates of point A be (x,y) and point O (2,-3) be the center,
then,
$\text{By mid-point formula,}\space\space\space\space\space\space\space\space \dfrac{x+1}{2}=\text{2 and }\dfrac{y+4}{2}=-3 \\[4.5 bp]$ or x = 4 - 1 and y =- 6 - 4
$\Rightarrow \space\space\space\space\space\space\space\space \text{x = 3 and y = - 10} \\[4.5 bp]$

\therefore \space\space\space\space\space\space \text{The coordinates of point A are (3,- 10)}

Q4. The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, – 5) and R(– 3, 6), find the coordinates of P.

Explanation:
Let the coordinates of point P be (2y, y). Since , P is equidistant from Q and R.
$\therefore \space\space\space\space\space\space\space\space PQ = PR \\[4.5 bp] \Rightarrow \space\space\space\space\space\space\space\space \sqrt{(2y-2)^2+(y+5)^2}=\sqrt{(2y+3)^2 + (y-6)^2}\\[4.5 bp] \Rightarrow \space\space\space\space\space\space\space\space (2y-2)^2 + (y + 5)^2= (2y + 3)^2 + (y - 6)^2 \\[4.5 bp] \Rightarrow \space\space\space\space\space\space\space\space 4y^2 + 4 - 8y + y^2 + 25 + 10y = 4y^2 + 9 + 12y + y^2 + 36 - 12y \\[4.5 bp] \Rightarrow \space\space\space\space\space\space\space\space 2y + 29 = 45 \\[4.5 bp] \Rightarrow \space\space\space\space\space\space\space\space 2y = 45 - 29 \\[4.5 bp] \Rightarrow \space\space\space\space\space\space\space\space y=\dfrac{16}{2} = 8$

Hence, the coordinates of point P are (16,8).

Q5. Determine the ratio in which the line x – y – 2 = 0 divides the line segment joining the points A(3, – 1) and B(8, 9).

Explanation:
Given, A = (3, – 1), B = (8, 9) and x – y – 2 = 0

Let the line x – y – 2 = 0 intersect the line segment AB at R in the ratio p : 1.

Now, $Rx = \dfrac{1(3)+p(8)}{p+1} \space \space and \space \space R_y =\dfrac{1(-1)+p(9)}{p+1} \\[4.5 bp] \Rightarrow \space\space R_x =\dfrac{3+8p}{p+1} \space\space and \space\space R_y =\dfrac{-1+9p}{p+1}\\[4.5 bp] \text{Thus,} \space \space R = \begin{pmatrix} \dfrac{3+8p}{p+1},\dfrac{9p-1}{p+1} \end{pmatrix} \\[4.5 bp]$

Now substituting the value of R in the given equation,

\text{we get} \\[4.5 bp] \dfrac{3+8p}{p+1}-\dfrac{9p-1}{p+1}-2=0 \\[4.5 bp] \Rightarrow\space\space\space\space 3 + 8p – 9p + 1 – 2(p + 1) = 0 \\[4.5 bp] \Rightarrow\space\space\space\space 4 – p – 2p – 2 = 0 \\[4.5 bp] \Rightarrow\space\space\space\space 3p = 2 \\[4.5 bp] \Rightarrow\space\space\space\space P=\dfrac{2}{3}\\[4.5 bp] \text{Thus, the ratio is} \space \dfrac{2}{3} : 1 = 2 : 3.

CBSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Real Numbers
Chapter 2	Polynomials
Chapter 3	Pair of Linear Equations in Two Variable
Chapter 4	Quadratic Equations
Chapter 5	Arithmetic Progressions
Chapter 6	Triangles
Chapter 7	Coordinate Geometry
Chapter 8	Introduction to Trigonometry
Chapter 9	Some Applications of Trigonometry
Chapter 10	Circles
Chapter 11	Areas Related to Circle
Chapter 12	Surface Areas and Volumes
Chapter 13	Statistics
Chapter 14	Probability

Conclusion

To improve your understanding of the chapter’s concepts, oswal.io offers a wide range of practice questions. Their extensive question bank is designed to help you reinforce your knowledge and enhance your problem-solving skills. By using these resources, you can strengthen your grasp of the topics and become better at solving various types of problems.

Frequently Asked Questions

Q1: What is Coordinate Geometry?

Ans: Coordinate Geometry is a branch of mathematics that involves the study of geometric figures using coordinate systems. It relates algebraic equations to geometric shapes and positions them on a coordinate plane.

Q2: What are the coordinates of the origin?

Ans: The coordinates of the origin are (0, 0). It is the point where the x-axis and y-axis intersect.

Q3: How do you find the distance between two points on the coordinate plane?

Ans: The distance between two points

(x_1, y_1)

and

(x_2, y_2)

on the coordinate plane can be calculated using the Distance Formula: Distance = √[(x₂ – x₁)² + (y₂ – y₁)²]

Q4: State the Section Formula for internal division.

Ans: The Section Formula for internal division gives the coordinates (x, y) of a point P that divides a line segment joining two points A(x₁, y₁) and B(x₂, y₂) in a given ratio ‘m:n’ internally as: x = [(mx₂ + nx₁)/(m + n)], y = [(my₂ + ny₁)/(m + n)]

Q5: What is the importance of the x-axis and y-axis in the coordinate plane?

Ans: The x-axis and y-axis are essential components of the coordinate plane. The x-axis represents the horizontal axis, and the y-axis represents the vertical axis. They intersect at the origin (0, 0). The coordinates of any point on the plane are determined by its position along these two axes.

Chapter Wise Important Questions for CBSE Board Class 10 Maths
Real Numbers
Polynomials
Pair of Linear Equations in Two Variables
Quadratic Equations
Arithmetic Progressions
Triangles
Coordinate Geometry
Introduction to Trigonometry
Some Applications of Trigonometry
Circles
Areas Related to Circles
Surface Areas and Volumes
Statistics
Probability

Class 10 Math Chapter 7 Coordinate Geometry

Introduction

What are Coordinate Geometry?

Class 10 Coordinate Geometry Important Questions and Answers

Q1. In the second quadrant, for a point, the abscissais ........... and the ordinate is ........... .

Options

(a) positive, negative (b) negative, positive (c) negative, negative (d) positive, positive

Q2. What is the ratio in which the line joining the points (6, 4) and (1, – 7) is divided by the X-axis?

Options

(a) 5 : 4 (b) 4 : 7 (c) 7 : 4 (d) 4 : 5

Q3. Find the coordinates of point A, where AB is the diameter of a circle whose center is (2, – 3) and B is the point (1,4).

Q4. The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, – 5) and R(– 3, 6), find the coordinates of P.

Q5. Determine the ratio in which the line x – y – 2 = 0 divides the line segment joining the points A(3, – 1) and B(8, 9).

CBSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1: What is Coordinate Geometry?

Q2: What are the coordinates of the origin?

Q3: How do you find the distance between two points on the coordinate plane?

Q4: State the Section Formula for internal division.

Q5: What is the importance of the x-axis and y-axis in the coordinate plane?

Class 10 Math Chapter 7
Coordinate Geometry

(a) positive, negative
(b) negative, positive
(c) negative, negative
(d) positive, positive

(a) 5 : 4
(b) 4 : 7
(c) 7 : 4
(d) 4 : 5