Class 10 Math Chapter 11
Areas Related To Circles
Important Questions

Here are some important questions for Class 10 Mathematics Chapter 11, Areas Related to Circles, carefully selected to help students prepare effectively for the CBSE Class 10 Mathematics Examination in 2024-25. By practicing these varied problems, students can better understand the concepts of Areas Related to Circles and improve their problem-solving skills. These questions aim to clarify doubts and enhance performance in the chapter.

Table of Contents

Introduction

In Chapter 11 of Class 10 Mathematics, Areas Related To Circles, we explore concepts related to the Area of Sectors and Segments of a circle. The problems in this chapter focus on calculating the areas and perimeters (or circumferences) of these plane figures. When calculating the area of a segment of a circle, the problems are restricted to central angles of 60°, 90°, and 120°. This chapter delves into understanding how to find the areas of different portions of a circle, as well as solving problems that involve both areas and perimeters/circumferences.

What is the area of a sector of a circle?

Ans: The area of a sector of a circle is the region enclosed by an arc and two radii of the circle. It is calculated using the formula,

A = (θ/360) × πr²,\\

where ‘θ’ is the central angle and ‘r’ is the radius.

Class 10 Areas Related To Circles Important Questions and Answers:

Q1. In the given figure, if ∠AOD = 135°, then ∠BOC is equal to:

(a) 52.5°
(b) 45°
(c) 62.5°
(d) 25°

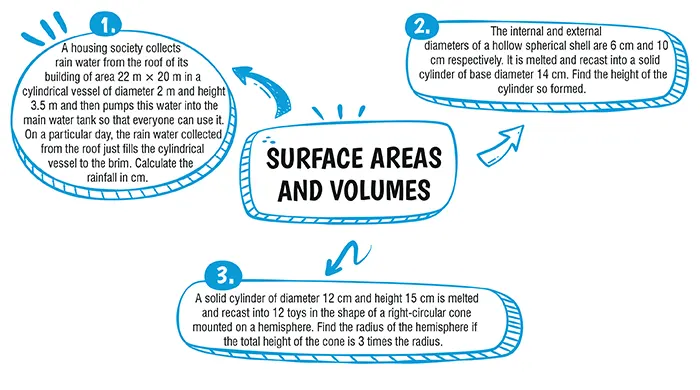
Ans.(b) 45°
Explanation:
Given, ∠AOD = 135°
∴ ∠BOC = 180° – 135° = 45°
Since, angles subtended at the center by a pair of opposite sides are supplementary.

Q2. To show the minor segment of a circle, a student shades the region enclosed between a chord and the minor arc. Which of these shows the region the student could have shaded?

Options

(a)

(b)

(c)

(d)

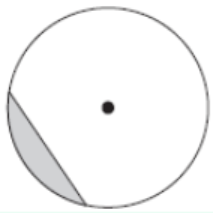
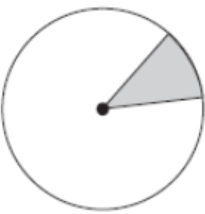
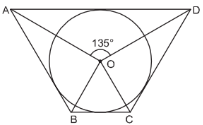
Ans. (a)

Explanation:
The shaded region consists of a chord and the arcs of the circle. The region in the white has the major arc, so it is the major segment and the shaded region consists of the minor arc, so it is the minor segment.

Q3. From each of the two adjacent corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the given figure. Find the area of the remaining portion of the square.

$\bigg (\text{Use π =} \dfrac{22}{7} \bigg)$

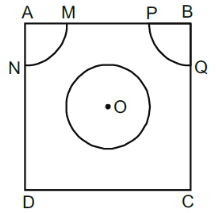
Explanation:

Given, AB = BC = CD = DA = 8 cm,
AM = AN = PB = QB = 1.4 cm and radius of circle with center O = 4.2 cm
Thus, area of the remaining portion
= Area of ABCD
- [Area of circle + 2 Area of quadrants] $\\= 8 × 8 - \bigg \{\dfrac{22}{7}(4.2)^2 + 2 × \dfrac{1}{4}× \dfrac{22}{7} (1.4)^2 \bigg\}\\ \text{= 64 - (55.44 + 3.08) cm}^2\\ \text{= 5.48 cm}^2$

Q4. The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.

Explanation:
Given, length of the minute hand = r = 14 cm
Total number of divisions in the clock = 12
Hence the angle subtended at the center between two digits covering five minutes = $\dfrac{360^o}{12}= 30^o\\$ Hence, area swept by the minute hand in covering 5 minutes $\\ = \dfrac{\theta}{360^o} \pi r^2 \\[5.5 bp] = \dfrac{30^o}{360^o} × \dfrac{22}{7}× (14)^2\\[5.5 bp] =\dfrac{154}{3} \\[5.5 bp] = 51.33 cm^2.$

Q5. From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed as shown in the figure. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of the remaining part of the metal sheet.

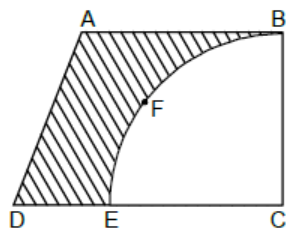
Explanation:
Given, AB =BC =3.5 cm and DE = 2 cm
As BC and EC are the radii of the circle, so
BC = EC
Thus, DC = (3.5+2) cm
= 5.5 cm
Hence , area of remaining part of the metal sheet
= Area of the trapezium - Area of the quadrant
$= \dfrac{1}{2}× \text{(sum of parallel sides)}\\[4.5 bp] × \text{(distance between parallel sides )-} \dfrac{1}{4}\pi r^2 \\[4.5 bp] = \dfrac{1}{2} (3.5 + 5.5)× 3.5 - \dfrac{1}{4} × \dfrac{22}{7} × (3.5)^2 \\[4.5 bp]= \dfrac{1}{2}× 9 × 3.5 - \dfrac{11×0.5×3.5}{2}\\[4.5 bp]= \dfrac{31.5}{2}-\dfrac{19.25}{2}\\[4.5 bp] = \dfrac{12.25}{2}\\[4.5 bp] = 6.125 \text{cm}^2$

CBSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Real Numbers
Chapter 2	Polynomials
Chapter 3	Pair of Linear Equations in Two Variable
Chapter 4	Quadratic Equations
Chapter 5	Arithmetic Progressions
Chapter 6	Triangles
Chapter 7	Coordinate Geometry
Chapter 8	Introduction to Trigonometry
Chapter 9	Some Applications of Trigonometry
Chapter 10	Circles
Chapter 11	Areas Related to Circle
Chapter 12	Surface Areas and Volumes
Chapter 13	Statistics
Chapter 14	Probability

Conclusion

To enhance your understanding of the Areas Related to Circles chapter, consider exploring oswal.io. This website provides a variety of practice questions designed to facilitate effective learning. By working on these questions, you can improve your grasp of circle-related concepts and enhance your problem-solving skills in this crucial math topic.

Chapter Wise Important Questions for CBSE Board Class 10 Maths
Real Numbers
Polynomials
Pair of Linear Equations in Two Variables
Quadratic Equations
Arithmetic Progressions
Triangles
Coordinate Geometry
Introduction to Trigonometry
Some Applications of Trigonometry
Circles
Areas Related to Circles
Surface Areas and Volumes
Statistics
Probability

Class 10 Math Chapter 11
Areas Related To Circles
Important Questions

Introduction

What is the area of a sector of a circle?