Trigonometry

Home / Board / ICSE / important Questions / Class 10 / Maths / Trigonometry

Class 10 Maths Chapter 18
Trigonometry
Important Questions

In Class 10 ICSE (Indian Certificate of Secondary Education) mathematics, Chapter 2 may not specifically cover the topic of “Banking” as its primary focus. Instead, the curriculum typically includes topics related to commercial mathematics, which can encompass banking concepts. Commercial mathematics includes areas such as simple interest, compound interest, and profit and loss, which are essential aspects of banking and finance. Here are trigonometric identities class 10 ICSE important questions.

Table of Contents

Introduction

In Class 10 ICSE (Indian Certificate of Secondary Education) mathematics, the chapter on “Trigonometry” is a fundamental topic that explores the relationships between angles and sides of right triangles. Trigonometry is a branch of mathematics that has wide-ranging applications, including in navigation, engineering, physics, and more. Here’s an introduction to trigonometry in Class 10 ICSE mathematics: Importance of Trigonometry: Trigonometry is a critical branch of mathematics because it helps us solve real-world problems involving angles and distances. It’s especially valuable in fields that require precise measurements and calculations. Common Trigonometric Formulas: Trigonometric Identities: These include the Pythagorean identities

(sin^2θ + cos^2θ = 1)

and various angle sum and difference identities. Special Angles: Trigonometry deals with special angles like 30 degrees, 45 degrees, and 60 degrees, which have well-defined trigonometric values.

What is Trigonometry?

Trigonometry is the study of the relationships between the angles and sides of triangles. It primarily focuses on right triangles, which have one angle equal to 90 degrees. Trigonometric functions and ratios, such as sine, cosine, and tangent, are used to establish these relationships. Key Concepts and Objectives:
Trigonometric Ratios: The fundamental trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). They relate the angles of a right triangle to the lengths of its sides.
Right Triangles: Trigonometry primarily deals with right triangles, where one angle is 90 degrees. The side opposite the right angle is the hypotenuse, and the other two sides are the legs.
Sine, Cosine, and Tangent: These trigonometric ratios are defined as follows:
Sine (sin): Opposite side / Hypotenuse
Cosine (cos): Adjacent side / Hypotenuse
Tangent (tan): Opposite side / Adjacent side

Class 10 Trigonometry Important Questions and Answers

Q1. $\space \space \frac{cos A}{1-sin A} - tan A =$

Options

(a) cos A
(b) sec A
(c) sin A
(d) cosec A

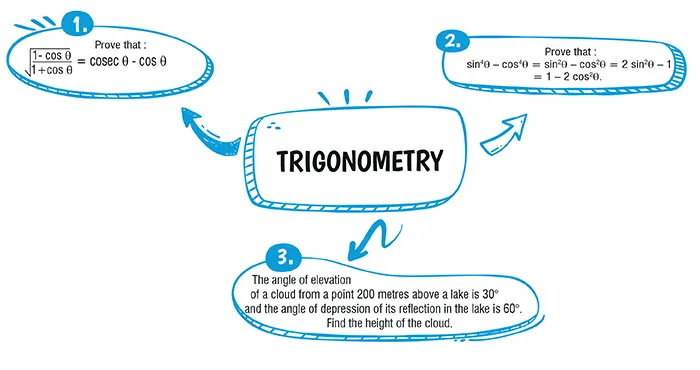
Ans. (b)
Explanation:
$\frac{cos A}{1- sin A} - tan A \\ = \frac{cos A(1+sin A)}{1-sin A(1+ sin A)}- tan A \\ =\frac{cos A(1+ sin A)}{(1+sin^2 A)} -tan A \\ = \frac{cos A(1+ sin A)}{cos^2 A} - tan A \\ = \frac{(1+sin A)}{cos A} -tan A \\ = \frac{1}{cos A} + \frac{sin A}{cos A} - tan A$

Q2. $\frac{cos A}{1-sin A} -tan A=$

Options

(a) Cos A
(b) Sec A
(c) Sin A
(d) Cosec A

Ans. (b)
Explanation:
$\frac{cos A}{1-sin A} -tan A = \frac{cos A(1+ sin A)}{(1- sin A)(1+ sin A)} - tan A \\ = \frac{cos A(1+sin A)}{1+sin^2 A} - tan A \\ = \frac{cos A(1+ sin A)}{cos ^2 A} - tan A \\ = \frac{1+ sin A}{cos A} - tan A \\ = \frac{1}{cos A} + \frac{sin A}{cos A} - tan A \\$ = sec A + tan A - tan A = sec A.

Q3. Prove that :

(i) $\sqrt{\frac{1-cos\theta}{1+cos \theta}} = cosec θ - cos θ \\ (ii) \sqrt{\frac{1+cos \theta}{1-cos \theta}} = sec θ - tan θ$

Explanation:
(i) L.H.S.
$=\sqrt{\frac{1-cos\theta}{1+cos\theta}×\frac{1-cos\theta}{1-cos\theta}} \\ =\sqrt{\frac{(1-cos\theta)^2}{1+cos^2\theta}} \\ =\frac{1-cos\theta}{\sqrt{1-cos^2\theta}} \\ =\frac{1-cos\theta}{\sqrt{sin^2\theta}} \\ =\frac{1-cos \theta}{sin \theta}\\ =\frac{1}{sin \theta}-\frac{cos \theta}{sin \theta} \\ = cosec θ – cot θ \\ \text{= R.H.S. Hence Proved.} \\ \text{(ii)L.H.S.=} \sqrt{\frac{1+sin \theta}{1-sin\theta}×\frac{1+sin \theta}{1+sin\theta}} \\ =\sqrt{\frac{(1+sin\theta)^2}{1-sin^2\theta}} \\ = \frac{1+sin\theta}{cos\theta} = \frac{1}{cos\theta} + \frac{sin\theta}{cos \theta} \\$ = sec θ + tan θ = R.H.S. Hence Proved

Q4. Prove that :

$sin^4 θ - cos^4 θ = sin^2θ - cos^2θ = 2 sin^2θ - 1 = 1 - 2 cos^2θ.$

Explanation:
Consider,
$sin^4θ – cos^4θ = (sin^2 θ)^2 – (cos^2 θ)^2 \\ = (sin^2 θ – cos^2θ)(sin^2θ + cos^2θ) [∵ (a – b)(a + b) = a^2– b^2] \\ = (sin^2 θ – cos^2θ) × 1 [∵ sin^2θ+ cos^2θ= 1] \\ = sin^2θ – cos^2θ \\ = sin^2θ – (1 – sin^2θ) [∵cos^2θ = 1 – sin^2θ] \\ = sin^2θ – 1 + sin^2θ \\ = 2 sin^2θ – 1 \\ = 2(1 – cos^2θ) – 1 [∵ sin^2θ =1 – cos^2θ] \\ = 2 – 2 cos^2θ – 1 \\ = 1 – 2 cos^2θ.$ Hence Proved.

Q5. The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.

Explanation:
Let P be the point of observation and C, the position of cloud. CN perpendicular from C on the surface of the lake and C‘ be the reflection of the cloud in the lake so that

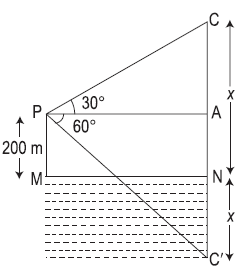
CN = NC´ = x (say)
Then, PM = 200 m
∴ AN = MP = 200 m
CA = CN – AN
= (x – 200) m
C´A = NC´ + AN
= (x + 200) m
Let PA = y m
Then, in right angled Δ PAC,
$\frac{CA}{PA} =tan 30 \\ ⟹ \frac{x+200}{y} = \sqrt{3} \\ ⇒x + 200 = \sqrt{3}y \\ ⟹ y = \frac{y+200}{\sqrt{3}} ...(ii) \\ \text{From equations (i) and (ii),}\\ \frac{x+200}{y} = \sqrt{3} (x-200)\\$ ⇒ x+200 = 3(x–200)
⇒ x+200 = 3x–600
⇒ 2x = 800
⇒ x = 400 m‍
Hence, the height of the cloud = 400 m.

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Want to Practice Mock Tests of this chapter

Download Important Questions of this chapter

ICSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Goods and Service Tax (GST)
Chapter 2	Banking
Chapter 3	Shares and Dividends
Chapter 4	Linear inequations
Chapter 5	Quadratic Equations in one variable
Chapter 6	Ratio and proportion
Chapter 7	Factorization
Chapter 8	Matrices
Chapter 9	Arithmetic Progression
Chapter 10	Geometric Progression
Chapter 11	Coordinate Geometry
Chapter 12	Reflection
Chapter 13	Similarity
Chapter 14	Loci
Chapter 15	Circles
Chapter 16	Constructions
Chapter 17	Mensuration
Chapter 18	Trigonometry
Chapter 19	Statistics
Chapter 20	Probability

Conclusion

The study of trigonometry in Class 10 ICSE mathematics is essential for understanding the relationships between angles and sides in right triangles. It equips students with tools to solve practical problems and lays the foundation for more advanced mathematics and scientific applications. If you seek additional practice and a deeper comprehension of the topics covered in the chapter, oswal.io offers an extensive array of class 10 Trigonometry important questions and answers to facilitate a more profound understanding of the concepts.

Chapter Wise Important Questions for ICSE Board Class 10 Mathematics
Goods and Service Tax (GST)
Banking
Shares and Dividends
Linear inequations
Quadratic Equations in one variable
Ratio and proportion
Factorization
Matrices
Arithmetic Progression
Geometric Progression
Coordinate Geometry
Reflection
Similarity
Loci
Circles
Constructions
Mensuration
Trigonometry
Statistics
Probability

Class 10 Maths Chapter 18
Trigonometry
Important Questions

Introduction

What is Trigonometry?

Class 10 Trigonometry Important Questions and Answers

Q1. $\space \space \frac{cos A}{1-sin A} - tan A =$

Options

(a) cos A
(b) sec A
(c) sin A
(d) cosec A

Q2. $\frac{cos A}{1-sin A} -tan A=$

Options

(a) Cos A
(b) Sec A
(c) Sin A
(d) Cosec A

Q3. Prove that :

(i) $\sqrt{\frac{1-cos\theta}{1+cos \theta}} = cosec θ - cos θ \\ (ii) \sqrt{\frac{1+cos \theta}{1-cos \theta}} = sec θ - tan θ$

Q4. Prove that :

$sin^4 θ - cos^4 θ = sin^2θ - cos^2θ = 2 sin^2θ - 1 = 1 - 2 cos^2θ.$

Q5. The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.

ICSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. What is trigonometry, and why is it important?

Q2. What are the primary trigonometric ratios?

Q3. What is the sine of an angle in a right triangle?

Q4. What is the cosine of an angle in a right triangle?

Q5. How is the tangent of an angle calculated in a right triangle?

Contact Us

Class 10 Maths Chapter 18 Trigonometry Important Questions

Introduction

What is Trigonometry?

Class 10 Trigonometry Important Questions and Answers

Q1. \space \space \frac{cos A}{1-sin A} - tan A =

Options

(a) cos A(b) sec A(c) sin A(d) cosec A

Q2. \frac{cos A}{1-sin A} -tan A=

Options

(a) Cos A(b) Sec A(c) Sin A(d) Cosec A

Q3. Prove that :

(i) \sqrt{\frac{1-cos\theta}{1+cos \theta}} = cosec θ - cos θ \\ (ii) \sqrt{\frac{1+cos \theta}{1-cos \theta}} = sec θ - tan θ

Q4. Prove that :

sin^4 θ – cos^4 θ = sin^2θ – cos^2θ = 2 sin^2θ – 1 = 1 – 2 cos^2θ.

Q5. The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.

ICSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. What is trigonometry, and why is it important?

Q2. What are the primary trigonometric ratios?

Q3. What is the sine of an angle in a right triangle?

Q4. What is the cosine of an angle in a right triangle?

Q5. How is the tangent of an angle calculated in a right triangle?

Contact Us

Class 10 Maths Chapter 18
Trigonometry
Important Questions

Q1. $\space \space \frac{cos A}{1-sin A} - tan A =$

(a) cos A
(b) sec A
(c) sin A
(d) cosec A

Q2. $\frac{cos A}{1-sin A} -tan A=$

(a) Cos A
(b) Sec A
(c) Sin A
(d) Cosec A

(i) $\sqrt{\frac{1-cos\theta}{1+cos \theta}} = cosec θ - cos θ \\ (ii) \sqrt{\frac{1+cos \theta}{1-cos \theta}} = sec θ - tan θ$

$sin^4 θ - cos^4 θ = sin^2θ - cos^2θ = 2 sin^2θ - 1 = 1 - 2 cos^2θ.$