Log in
Log in
Start Free Trial
Constructions

Home / Board / ICSE / important Questions / Class 10 / Maths / Constructions

Class 10 Maths Chapter 13
Constructions
Important Questions

exam preparation with oswal.io
In mathematics, construction typically refers to the act of drawing geometric shapes using only a compass and a straightedge. This ancient practice has roots in Greek mathematics and is deeply connected with the field of classical geometry.These constructions are fundamental in geometry and provide a hands-on approach to solving geometric problems. Class 10 construction important questions and answers are designed as a valuable tool to help students build confidence in their mathematical skills.

Introduction

The chapter on “Constructions” is an essential part of geometry. This chapter teaches students how to create various geometric shapes and figures using only a compass and straightedge. Constructions are crucial because they not only enhance students’ problem-solving skills but also lay the foundation for more advanced geometric concepts. Constructions involve using two primary tools—the compass, which is used to draw circles and arcs, and the straightedge, which is a ruler without markings. These tools are used to create accurate geometric shapes and solve problems. In construction problems, you do not use numerical measurements like lengths or angles. Instead, you rely on the properties of geometric figures and relationships between them. These concepts are crucial when studying Class 10 construction important questions and answers.

What is Constructions?

Constructions in mathematics refer to the process of creating geometric figures or shapes using precise steps and tools—typically, a compass and a straightedge. The goal of constructions is to create these figures accurately without relying on measurements or numerical values.
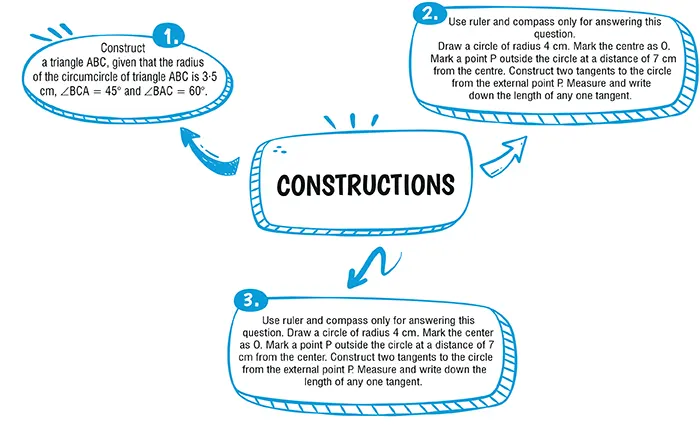
Math Chapter 16 01

Class 10 Constructions Important Questions and Answers

Q1. In the given figure find the radius of circle:
construction Q1
Options
(a) 2 cm
(b) 5 cm
(c) 4 cm
(d) 3 cm

Ans. (b) 5 cm
Explanation:
△AOB is a right angle triangle.
∴ by pythagoras theorem
(OA)^2 = (OB)^2 - (AB)^2\\ OA = (13)^2 - (12)^2 OA = 169 - 144 = 25
= 5 cm.

Q2. In the given figure, DC = 6 cm, AC = 9 cm and find AB.
Construction_Q2
Options
(a) 4 cm
(b) 5 cm
(c) 9 cm
(d) 10 cm

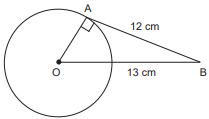
Ans. (b) 5 cm
Explanation:
As we know that
(DC)^2 = AC × BC \\ (6)^2 = 9 × BC BC = 369 = 4 cm.
Now AB = AC – BC
= 9 – 4
AB = 5 cm

Q3. Construct a triangle ABC, given that the radius of the circumcircle of triangle ABC is 3·5 cm, ∠BCA = 45° and ∠BAC = 60°.
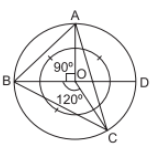
construction_Q3

Explanation:
Steps of construction :
(i) Draw a circle with radius = 3·5 cm.
(ii) Draw diameter BOD and construct ∠BOA = 90°.
(iii) Again make ∠BOC = 120°.
(iv) Join AB, AC and BC. Then, ABC is the required triangle

Q4. Use ruler and compass only for answering this question. Draw a circle of radius 4 cm. Mark the centre as O. Mark a point P outside the circle at a distance of 7 cm from the centre. Construct two tangents to the circle from the external point P. Measure and write down the length of any one tangent.
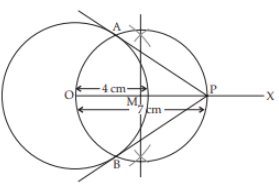
construction Q4

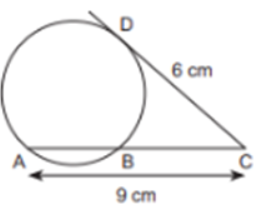
Explanation:
Given, radius = 4 cm and OP = 7 cm
Steps of constructions :
(i) Draw a circle of radius 4 cm with centre at O.
(ii) Draw a line OX and cut-off OP = 7 cm.
(iii) Bisect OP at M.
(iv) With M as centre, draw a circle passing through the points O and P to cut the previous circle at A and B.
(v) Join P with A and B. Hence, AP and BP are the required tangents.
∴ The length of tangent, AP = 5.7 cm

Q5. Using ruler and compass only, construct a triangle ABC such that AB = 5 cm, ∠ABC = 75° and the radius of the circumcircle of triangle ABC is 3·5 cm. On the same diagram, construct a circle, touching AB at its middle point and also touching the side AC.
(a) Slope of BC,
(b) Equation of a line perpendicular of BC and passing through A.
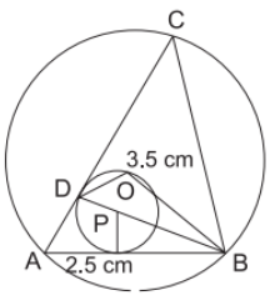
constructionQ5

Explanation:
Steps of construction :
(i) Draw a line segment AB = 5 cm long.
(ii) Make an angle of 75° at ‘B’ draw perpen -dicular bisector of AB and angular bisector of B.
(iii) Mark 3·5 cm on the perpendicular bisector with O as center and radius equal to OA or OB draw circumcircle.
(iv) Mark 2·5 cm on AC from A.
(v) Join BD, it will intersect at P, with P as centre and PD as radius draw another circle.

Want to Master this Chapter?
Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now
Want to Master this Chapter?
Our Practice Tests, Mind Maps, and Key Questions will help!
Download Mind Map of this chapter
Download Now
Want to Practice Mock Tests of this chapter
Practice Now
Download Important Questions of this chapter
Download Now

ICSE Class 10 Maths Chapter wise Important Questions

Chapter No.Chapter Name
Chapter 1Goods and Service Tax (GST)
Chapter 2Banking
Chapter 3Shares and Dividends
Chapter 4Linear inequations
Chapter 5Quadratic Equations in one variable
Chapter 6Ratio and proportion
Chapter 7Factorization
Chapter 8Matrices
Chapter 9Arithmetic Progression
Chapter 10Geometric Progression
Chapter 11Coordinate Geometry
Chapter 12Reflection
Chapter 13Similarity
Chapter 14Loci
Chapter 15Circles
Chapter 16Constructions
Chapter 17Mensuration
Chapter 18Trigonometry
Chapter 19Statistics
Chapter 20Probability

Conclusion

Construction of class 10 ICSE mathematics is like a toolbox for students to create precise shapes and figures in geometry. If you seek additional practice and a deeper comprehension of the topics covered in the chapter, oswal.io offers an extensive array of ICSE maths class 10 construction to facilitate a more profound understanding of the concepts.

Frequently Asked Questions

Ans: Constructions in mathematics are methods for creating geometric figures using only a compass and a straightedge, without using measurements or numerical values.
Ans: Constructions help students understand geometric concepts, develop problem-solving skills, and have real-world applications in fields like engineering and architecture.
Ans: The primary tools used in constructions are a compass (for drawing circles and arcs) and a straightedge (a ruler without markings).
Ans: Bisecting an angle means dividing it into two equal parts. This skill is used in various geometric constructions and to create angles of specific measurements.
Ans: To draw a perpendicular bisector, use a compass to create arcs on both sides of the line segment. Then, draw two arcs of equal radius above and below the segment. The intersection points are the endpoints of the perpendicular bisector.
logo1
Instagram Linkedin-in Facebook-f Youtube Twitter
Instagram Linkedin-in Facebook-f Youtube Twitter
  • Syllabus
  • Blogs
  • Plans
  • Contact Us
  • Privacy Policy

CBSE Important Questions Class 9

CBSE Important Questions Class 10

CBSE Important Questions Class 12

CBSE Practice Papers

CBSE Practice Papers

ICSE Important Questions Class 9

  • ICSE Class 9 Maths
  • ICSE Class 9 Physics
  • ICSE Class 9 Chemistry
  • ICSE Class 9 Biolog1y
  • ICSE Class 9 History & Civics
  • ICSE Class 9 Geography
  • ICSE Class 9 Computer Applications

ICSE Important Questions Class 10

ICSE Practice Papers

  • ICSE Class 10 Physics
  • ICSE Class 10 Chemistry
  • ICSE Class 10 Biology
  • ICSE Class 10 Maths

ISC Important Questions Class 12

ISC Practice Papers

  • ISC Class 12 Physics
  • ISC Class 12 Chemistry
  • ISC Class 12 Biology
  • ISC Class 12 Maths

Contact Us

Head Office : Ground Floor, 1 / 12 Sahitya Kunj, M.G Road Agra 282002, Uttar Pradesh (India)
Phone No.: +91-562 25277711
Mobile No.: +91-7455077222
Email: support@oswalpublishers.in
Corporate Office : Noida One, B 702, B7, Sector 62,
Noida - 201309, Uttar Pradesh
Phone No.: +91-562 25277711
Mobile No.: +91-75348 77222
Email: support@oswalpublishers.in

© Copyright 2024 oswal.io by OSWAL PUBLISHERS Simplifying Exams