Linear Inequation

Home / Board / ICSE / important Questions / Class 10 / Maths / linear inequations

Class 10 Maths Chapter 3
Linear Inequation
Important Questions

Q: Q1. What is a linear inequality?

Ans: A linear inequality is a mathematical statement that involves linear functions and comparison operators to represent relationships between two expressions, indicating that one is less than, greater than, less than, or equal to, or greater than or equal to the other.

Q: Q2. How do you solve a linear inequality?

Ans: To solve a linear inequality, perform operations like addition, subtraction, multiplication, or division on both sides while considering the direction of the inequality sign. The result will yield the valid values for the variable (s).

Q: Q3. What is the solution set of a linear inequality?

Ans: The solution set of a linear inequality is the set of all values of the variable (s) that satisfy the inequality, making it true. It can be represented as a range of values.

Q: Q4. How do you graphically represent a linear inequality?

Ans: To graphically represent a linear inequality, plot the boundary line (usually a straight line) corresponding to the equation formed by the inequality. Then, shade the region above or below the line to indicate the solution set.

Q: Q5. Can a linear inequality have no solution?

Ans: Yes, a linear inequality can have no solution if there is no range of values for the variable (s) that satisfies the inequality. This occurs when the solution region on the graph is empty.

Class 10 Linear inequalities are a fundamental topic in mathematics, playing a pivotal role in solving real-world problems and understanding mathematical concepts. A solid grasp of linear inequalities is essential for success in ICSE Class 10 mathematics. In this collection of important questions, we will delve into the core concepts of linear inequalities, covering a wide range of problem types. These linear inequations class 10 ICSE questions are designed to help you practice and prepare effectively, ensuring that you are well-equipped to handle linear inequalities with confidence. ‍ Solving Linear Inequalities: a. Solve the inequality: 2x – 5 < 7. b. Determine the solution set for 3(x + 4) ≥ 15. c. Solve the inequality: 2(x – 3) < 4x + 5. Graphical Representation: a. Graph the inequality: 2x + 3y ≤ 6. b. Illustrate the solution set for the inequality: x > -2.

Table of Contents

Introduction

A linear inequality in linear inequations class 10 icse is an expression involving linear functions (polynomials of degree 1) and comparison operators (such as <, >, ≤, or ≥). Unlike linear equations, which equate two expressions, linear inequalities establish a relationship between two expressions, indicating that one is less than, greater than, less than, or equal to, or greater than or equal to the other. Linear inequalities can be visually represented on a coordinate plane. The solutions lie either above or below a boundary line, depending on the inequality’s direction. Shading regions on the graph corresponding to the solution set provide a clear visualization of the valid solutions.

What is Linear Inequality?

linear inequalities, often referred to as “linear inequations,” are mathematical expressions or statements that involve linear functions and a comparison operator to establish a relationship between two mathematical expressions, indicating that one is less than, greater than, less than, or equal to, or greater than or equal to the other. These linear inequations are essential in modeling real-world situations with inequalities and constraints. Here are the key components and concepts related to linear inequations class 10 ICSE:Linear Functions: Linear functions are algebraic expressions that consist of constants, variables raised to the first power, and the basic operations of addition, subtraction, multiplication, and division. For example, expressions like 2x + 3, 4y – 1, and 0.5z are linear functions. Comparison Operators: Linear inequalities use comparison operators to define the relationship between two linear expressions. The commonly used operators are: < (less than) (greater than) ≤ (less than or equal to) ≥ (greater than or equal to) Linear Inequality Expressions: A linear inequality expression is typically written in the form: Linear Expression_1 Linear Expression_2 For example, 2x + 3 > 7 is a linear inequality where 2x + 3 and 7 are the linear expressions, and > is the comparison operator.Solving Linear Inequalities: Solving a linear inequality involves finding the values of the variable(s) that satisfy the inequality. The set of all valid solutions is called the “solution set.” To solve linear inequalities, you may need to manipulate the inequality by performing operations like addition, subtraction, multiplication, or division on both sides, just like solving equations. However, keep in mind that when you multiply or divide by a negative number, the direction of the inequality sign may change.

Class 10 Linear Inequality Important Questions and Answers

Q1. If 2x – 5 ≤ 5x + 4 < 29 and x is an integer, then the solution set of x is:

Options

(a) {– 2, – 1, 0, 1, 2, 3, 4, 5}
(b) {– 2, – 1, 0, 1, 2, 3, 4}
(c) {– 3, – 2, – 1, 0, 1, 2, 3, 4, 5}
(d) {– 3, – 2, – 1, 0, 1, 2, 3, 4}

Ans. (d) {– 3, – 2, – 1, 0, 1, 2, 3, 4}
Explanation:
We have
$2x-5 ≤ 5x+4 < 29, x ∈ I \\ ⇒ 2x-5 ≤ 5x+4; 5x + 4 < 29 \\ ⇒ 2x - 5x ≤ 4 + 5; 5x < 29 - 4 \\ ⇒ - 3x ≤ 9; 5x < 25 \\ ⇒\frac{-3x}{-3} ≥ \frac{9}{-3}; \frac{5x}{5} < \frac{25}{5} \\$ ⇒ x ≥ - 3; x < 5 ∴ x = {– 3, – 2, – 1, 0, 1, 2, 3, 4}

Q2. The solution set representing the following number line is:

Options

(a) {x : x ∈ R, –2 ≤ x < 3}
(b) {x : x ∈ R, –2 < x ≤ 3}
(c) {x : x ∈ R, –2 ≤ x ≤ 3}
(d) {x : x ∈ R, –2 < x < 3}

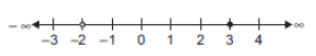
Ans. (b) {x : x ∈ R, –2 < x ≤ 3}
Explanation:
{x : x ∈ R, –2 < x ≤ 3} The adjacent figure shows x > - 2 and x ≤ 3
So, answer will be
{x : x ∈ R, -2 < x ≤ 3}

Q3. $\frac{-x}{3} \frac{x}{2} - \frac{4}{3}, < \frac{1}{6}, x\epsilon R$

\frac{-x}{3} \leq \frac{x}{2} - \frac{4}{3} < \frac{1}{6} \\ x \in \mathbb{R} \\ -2x \leq 3x - 8 < 1 \\ \text{Multiply by 6} \\ -12x \leq 18x - 48 < 6 \\ x \geq \frac{8}{5} \text{ and } x < 3 \\ \frac{8}{5} \leq x < 3, x \in \mathbb{R} \\ \text{Set} = \{ x : x \in \mathbb{R}, \frac{8}{5} \leq x < 3 \}

Q4. Solve the inequation and represent the solution it on the number line :

$\frac{x}{3} ≤ \frac{x}{3} 1 \frac{1}{3} < \frac{1}{6}, x ∈ R$

Explanation:
we have,
$\frac{x}{3} ≤ \frac{x}{3} 1 \frac{1}{3} < \frac{1}{6} , x ∈ R$

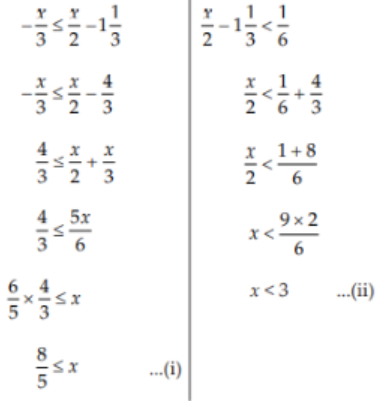
Now,
Thus, $\frac{8}{5} ≤ x < 3 \space Or \space 1.6 ≤ x < 3 \\ ∴ \text{Solution set =} [ x : 1.6 ≤ x < 3, ∈ R ].$

Q5. Solve the following inequation, and graph the solution on the number line:

$\frac{3x+15}{5} ≤ 2x + 3 ≤ \frac{3x+15}{2}, x ∈ R$

Explanation:
Taking L.C.M. of 5, 2 = 10 and on multiplying throughout by 10, we get:
$\frac{3x+15}{5} × 10 ≤ (2x + 3) × 10 ≤ \frac{3x+15}{2} \\ × 10 2(3x+15) ≤ 10(2x+3) ≤ 5(3x+15), \\$ which on simplification gives:
6x + 30 ≤ 20x + 30 ≤ 15x + 75,
Solving the LHS part:
6x + 30 ≤ 20x + 30
⇒ 14x ≥ 0
⇒ x ≥ 0...........(i)
Again, solving the RHS part: 10(2x+3) ≤ 5(3x+15)
⇒ 20x + 30 ≤ 15x + 75
⇒ 20x - 15x ≤ 75 - 30
⇒ 5x ≤ 45
$⇒ x ≤ \frac{45}{5}$ ⇒ x ≤ 9 ...........(ii)

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Want to Practice Mock Tests of this chapter

Download Important Questions of this chapter

ICSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Goods and Service Tax (GST)
Chapter 2	Banking
Chapter 3	Shares and Dividends
Chapter 4	Linear inequations
Chapter 5	Quadratic Equations in one variable
Chapter 6	Ratio and proportion
Chapter 7	Factorization
Chapter 8	Matrices
Chapter 9	Arithmetic Progression
Chapter 10	Geometric Progression
Chapter 11	Coordinate Geometry
Chapter 12	Reflection
Chapter 13	Similarity
Chapter 14	Loci
Chapter 15	Circles
Chapter 16	Constructions
Chapter 17	Mensuration
Chapter 18	Trigonometry
Chapter 19	Statistics
Chapter 20	Probability

Conclusion

In conclusion, linear inequations of linear inequations class 10 ICSE are a fundamental concept of Mathematics. They provide a powerful tool for modeling and solving real-world problems that involve inequalities, constraints, and decision-making. If you wish to improve your skills further and gain a better grasp of the concepts covered in this chapter, you can explore oswal.io, where you’ll find a wide range of practice questions. These linear inequations class 10 ICSE questions are designed to assist you in your journey to achieve a more in-depth understanding of the material.

Frequently Asked Questions

Q1. What is a linear inequality?

Ans: A linear inequality is a mathematical statement that involves linear functions and comparison operators to represent relationships between two expressions, indicating that one is less than, greater than, less than, or equal to, or greater than or equal to the other.

Chapter Wise Important Questions for ICSE Board Class 10 Mathematics
Goods and Service Tax (GST)
Banking
Shares and Dividends
Linear inequations
Quadratic Equations in one variable
Ratio and proportion
Factorization
Matrices
Arithmetic Progression
Geometric Progression
Coordinate Geometry
Reflection
Similarity
Loci
Circles
Constructions
Mensuration
Trigonometry
Statistics
Probability

Class 10 Maths Chapter 3 Linear Inequation Important Questions

Introduction

What is Linear Inequality?

Class 10 Linear Inequality Important Questions and Answers

Q1. If 2x – 5 ≤ 5x + 4 < 29 and x is an integer, then the solution set of x is:

Options

(a) {– 2, – 1, 0, 1, 2, 3, 4, 5}(b) {– 2, – 1, 0, 1, 2, 3, 4}(c) {– 3, – 2, – 1, 0, 1, 2, 3, 4, 5}(d) {– 3, – 2, – 1, 0, 1, 2, 3, 4}

Q2. The solution set representing the following number line is:

Options

(a) {x : x ∈ R, –2 ≤ x < 3}(b) {x : x ∈ R, –2 < x ≤ 3}(c) {x : x ∈ R, –2 ≤ x ≤ 3}(d) {x : x ∈ R, –2 < x < 3}

Q3. \frac{-x}{3} \frac{x}{2} - \frac{4}{3}, < \frac{1}{6}, x\epsilon R

Q4. Solve the inequation and represent the solution it on the number line :

\frac{x}{3} ≤ \frac{x}{3} 1 \frac{1}{3} < \frac{1}{6}, x ∈ R

Q5. Solve the following inequation, and graph the solution on the number line:

\frac{3x+15}{5} ≤ 2x + 3 ≤ \frac{3x+15}{2}, x ∈ R

ICSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. What is a linear inequality?

Q2. How do you solve a linear inequality?

Q3. What is the solution set of a linear inequality?

Q4. How do you graphically represent a linear inequality?

Q5. Can a linear inequality have no solution?

Class 10 Maths Chapter 3
Linear Inequation
Important Questions

(a) {– 2, – 1, 0, 1, 2, 3, 4, 5}
(b) {– 2, – 1, 0, 1, 2, 3, 4}
(c) {– 3, – 2, – 1, 0, 1, 2, 3, 4, 5}
(d) {– 3, – 2, – 1, 0, 1, 2, 3, 4}

(a) {x : x ∈ R, –2 ≤ x < 3}
(b) {x : x ∈ R, –2 < x ≤ 3}
(c) {x : x ∈ R, –2 ≤ x ≤ 3}
(d) {x : x ∈ R, –2 < x < 3}

Q3. $\frac{-x}{3} \frac{x}{2} - \frac{4}{3}, < \frac{1}{6}, x\epsilon R$

$\frac{x}{3} ≤ \frac{x}{3} 1 \frac{1}{3} < \frac{1}{6}, x ∈ R$

$\frac{3x+15}{5} ≤ 2x + 3 ≤ \frac{3x+15}{2}, x ∈ R$