logo
Log in
  Get Rs 200 off on Oswal Premium Plan this New Year! For Class 9th and 12th. Use Coupon Code NEWYEAR200 at checkout.
logo
Log in
Start Free Trial
Similarity

Home / Board / ICSE / important Questions / Class 10 / Maths / Similarity

Class 10 Maths Chapter 13
Similarity
Important Questions

exam preparation with oswal.io
The chapter on “Similarity” in ICSE Class 10 Mathematics explores the concept of geometric similarity, which is fundamental in solving various real-world problems. Students learn about similar triangles, a key topic in this chapter, and how to identify them using certain criteria like the Angle-Angle (AA) similarity criterion. Understanding the properties of similar figures, including polygons, circles, and their corresponding angles, is a crucial aspect of this chapter. The chapter delves into the applications of similarity in solving problems related to indirect measurement, such as height and distance calculations. Here’s an introductory overview of similarity class 10 ICSE board questions.

Introduction

In Similarity of class 10 ICSE chapter the concept of “Similarity” is a fundamental topic within the realm of geometry. This chapter explores the principles of similarity, which involves the comparison of geometric figures that have the same shape but possibly different sizes. ‍ Here’s an introductory overview of the concept of “Similarity” in ICSE Class 10 Mathematics: “In the world of geometry, ‘Similarity’ takes center stage in ICSE Class 10 Mathematics. This fundamental concept revolves around the comparison of shapes that share the same form or structure but may differ in size. Similarity plays a pivotal role in understanding relationships between geometric figures, from triangles to more complex shapes. Throughout this chapter, students will delve into the principles of similarity, exploring how to identify, prove, and apply similarity in various scenarios. The study of similarity not only enhances their geometric reasoning but also equips them with problem-solving skills that have practical applications in fields such as architecture, engineering, and design.

What is Similarity?

In ICSE Class 10 Mathematics, “similarity” is like finding twins among geometric shapes. It’s when shapes have the same form or structure but can be different in size. Imagine you have two triangles that look exactly alike, but one is larger than the other. They are similar because their shapes match, even though they’re not the same size. Similarity of class 10 ICSE means having the same shape, just like how identical twins have the same face, but one might be taller or shorter than the other. In geometry, we use similarity to compare shapes and figure out their proportions. It’s a handy tool for solving all sorts of real-world problems, from resizing pictures to designing buildings.
similarity questions class 10 icse

Class 10 Similarity Important Questions and Answers

Q1. In the given figure, ΔAPC ~ ΔBPD by which of the following similarity criterion?
Similarity_Q1
Options
(a) SAS
(b) SSS
(c) ASA
(d) AA

Ans. (d) AA
Explanation:
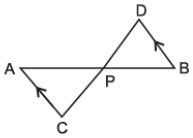
Here, In ΔAPC and ΔBPD
∠ APC= ∠ BPD [vertically opposite angles] ∠ ACP= ∠ BDP [Alternate Interior angles] ∴ By AA similarly
ΔAPC ~ ΔBPD

Q2. In the given figure, if ΔPQR ~ ΔPST, then
\frac{PQ}{PR}..............
Options
(a) \frac{PS}{PT} \\ (b) \frac{PT}{PS} \\ (c) \frac{PR}{PQ} \\ (d) \frac{PR}{PT}

Ans. (b)
Explanation:
Sol. ∵ ΔPQR ~ ΔPST,
∴ \frac{PQ}{PS}=\frac{QR}{ST}=\frac{PR}{PT} \\ ⇒\frac{PQ}{PS}= \frac{PR}{PT} \space \\ \text{Or} \space \space \frac{PQ}{PR}= \frac{PS}{PT}

Q3. On a map drawn to a scale of 1 : 50,000, a rectangular plot of land ABCD has the following dimensions. AB = 6 cm; BC = 8 cm and all angles are right angles. Find the actual area of the plot in sq. km.

Explanation:
Here,  1 : k = 1 : 50,000
and       AB = 6 cm, BC = 8 cm 

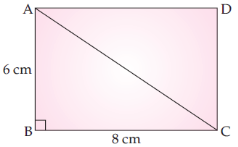
Similarity_Q3

Area of rectangle ABCD = 6 × 8 = 48 cm^2‍ \\ \text{∴ Actual area =} k^2 × \text{Area of ABCD}\\ = (50‚000)^2 × 48 cm^2 \\ = \frac{50,000×50,000×48}{1,00,000×1,00,000} km^2 \\ = 12 km^2.

Q4.Determine the ratio of the area of two similar triangles if one pair of their corresponding sides are 3 cm and 5 cm.

Explanation:
Let the two triangles be ABC and DEF
Let BC = 3 cm and EF = 5 cm.
Then, \frac{Area(\Delta ABC)}{Area(\Delta DEF)}=\frac{(BC)^2}{(BC)^2} = \frac{3^2}{5^2} = 9 : 25.

Q5. In DABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm, AD = 5 cm.
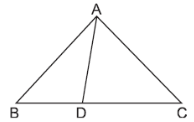
Similarity Q5
(i) Prove that ΔACD is similar to Δ BCA.
(ii) Find BC and CD.
(iii) Find area of ΔACD : area of ΔABC.

Explanation:
∠ABC = ∠DAC = x (say)
Given, AB = 8 cm, AC = 4 cm and AD = 5 cm.

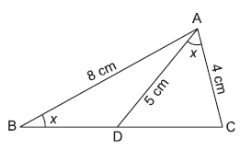
Similarity_ans5

(i) In Δ ACD and Δ BCA,
∠ ABC = ∠ DAC (Given)
∠ ACD = ∠ BCA (Common)
⇒ Δ ACD ~ Δ BCA (By AA axiom)
Hence, Δ ACD is similar to Δ BCA.(ii) As we have,
\frac{AC}{BC}=\frac{CD}{CA}=\frac{AD}{BA} \\ ⇒ \frac{4}{BC} = \frac{CD}{4} = \frac{5}{8} \\ ⇒ \frac{4}{BC} = \frac{5}{8} \\ ⇒ BC = \frac{8×4}{8} = \frac{32}{5} = 6 . 4 cm.\\ and \frac{CD}{4} = \frac{5}{8}\\ ⇒ CD = \frac{5×4}{8} = \frac{32}{5} = 2.5 cm. \\ (iii) \frac{Area\space of \Delta ACD}{Area\space of \Delta ABC}= \begin{pmatrix}\frac{AC}{AB} \end{pmatrix}^2 = \begin{pmatrix}\frac{4}{8} \end{pmatrix}^2=\frac{1}{4} \\ Thus, area of Δ ACD: area of Δ ABC = 1 : 4.

Want to Master this Chapter?
Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now
Want to Master this Chapter?
Our Practice Tests, Mind Maps, and Key Questions will help!
Download Mind Map of this chapter
Download Now
Want to Practice Mock Tests of this chapter
Practice Now
Download Important Questions of this chapter
Download Now

ICSE Class 10 Maths Chapter wise Important Questions

Chapter No.Chapter Name
Chapter 1Goods and Service Tax (GST)
Chapter 2Banking
Chapter 3Shares and Dividends
Chapter 4Linear inequations
Chapter 5Quadratic Equations in one variable
Chapter 6Ratio and proportion
Chapter 7Factorization
Chapter 8Matrices
Chapter 9Arithmetic Progression
Chapter 10Geometric Progression
Chapter 11Coordinate Geometry
Chapter 12Reflection
Chapter 13Similarity
Chapter 14Loci
Chapter 15Circles
Chapter 16Constructions
Chapter 17Mensuration
Chapter 18Trigonometry
Chapter 19Statistics
Chapter 20Probability

Conclusion

In conclusion, Similarity of class 10 ICSE the study of similarity in ICSE Class 10 Mathematics provides students with a powerful tool for understanding and comparing geometric figures that share the same shape but may differ in size. Throughout this chapter, students have explored the principles of similarity, discovering how to identify, prove, and apply it in various contexts. ‍ The concept of similarity not only enriches students’ geometric reasoning but also equips them with valuable problem-solving skills. It allows them to analyze and resize shapes while maintaining their proportions, which has practical applications in fields such as architecture, engineering, and design. ‍ If you want to get better at this chapter and really understand it, check out oswal.io. Oswal.io has lots of similarity questions class 10 ICSE to help you practice and get a deeper grasp of the ideas. It’s like having a treasure chest of knowledge to make you a math wizard!

Frequently Asked Questions

Ans: Similarity is a geometric concept where two or more figures have the same shape but may differ in size.
Ans: Two figures are similar if their corresponding angles are equal, and the ratios of their corresponding sides are in proportion.
Ans: Similarity is used for scaling and resizing objects, such as maps, architectural designs, and models, while preserving their proportions.
Ans: The ratio of corresponding sides in similar figures is called the “scale factor.”
Ans: Yes, all equilateral triangles are similar because they have the same shape and their angles are equal.
logo
Instagram Linkedin-in Facebook-f Youtube Twitter
logo
Instagram Linkedin-in Facebook-f Youtube Twitter

CBSE Important Questions Class 10

ICSE Important Questions Class 10

CBSE Important Questions Class 10

ICSE Important Questions Class 10

Contact Us

© Copyright 2024 oswal.io by OSWAL PUBLISHERS Simplifying Exams