Matrices

Home / Board / ICSE / important Questions / Class 10 / Maths / Matrices

Class 10 Maths Chapter 8
Matrices
Important Questions

In ICSE Class 10 Mathematics, Matrices embarks on a journey into the intriguing realm of matrices—a mathematical tool with wide-ranging applications in fields such as science, engineering, and computer science. Matrices, essentially organized arrays of numbers in rows and columns, form the core of this chapter’s exploration. This chapter introduces students to the fundamental concepts of matrices and unveils their real-world significance. Matrices play pivotal roles in solving systems of linear equations, analyzing data, and creating computer graphics, making them indispensable in various disciplines. Through this chapter, students acquire a solid foundation in matrix basics, matrix operations, determinants, and their practical utility in tackling everyday problems.

Table of Contents

Introduction

In the chapter matrices class 10, “Matrices” is a captivating subject that unlocks a potent mathematical tool. Picture matrices as organized grids, filled with numbers that hold specific positions in rows and columns. These grids may seem straightforward, but they wield immense power, finding applications in computer graphics, engineering, and practical problem-solving. As you delve into this chapter and solve matrices class 10 ICSE important questions you’ll embark on a journey into the intricate world of matrices. You’ll master the art of working with them, performing operations, and comprehend their profound significance. Matrices serve as the backbone for solving equations, dissecting data, and creating stunning visual effects in industries like entertainment and technology.

What is Matrices?

In the chapter matrices class 10 ICSE, a matrix, in its simplest form, is a rectangular arrangement or table of numbers, symbols, or expressions, organized into rows and columns. Each number or element within a matrix has a specific location, identified by its row and column. Matrices are fundamental mathematical objects used for various purposes, including solving systems of linear equations, data organization, computer graphics, and transformations in geometry.
Here are some key points to understand about matrices in ICSE Class 10 Mathematics:
Organization: A matrix is structured into rows and columns, much like a spreadsheet. The number of rows and columns in a matrix is referred to as its dimensions.
Elements: Each entry or element within a matrix is represented by a number or symbol. The elements of a matrix are typically denoted by letters with subscripts to indicate their position, such as “a₁₁” for the element in the first row and first column.
Types of Matrices: Matrices come in various forms, including square matrices (with an equal number of rows and columns), row matrices (with one row and multiple columns), and column matrices (with one column and multiple rows).

Class 10 Matrices Important Questions and Answers

Q1. If A = $\begin{bmatrix} 2 & 12 \\ 0 & 1 \end{bmatrix}, B = \begin{bmatrix} 4 & x \\ 0 & 1 \end{bmatrix} \space and \space A^2 = B,$ then the value of x is ...................... .
Options

(a) 48
(b) 52
(c) -26
(d) -24

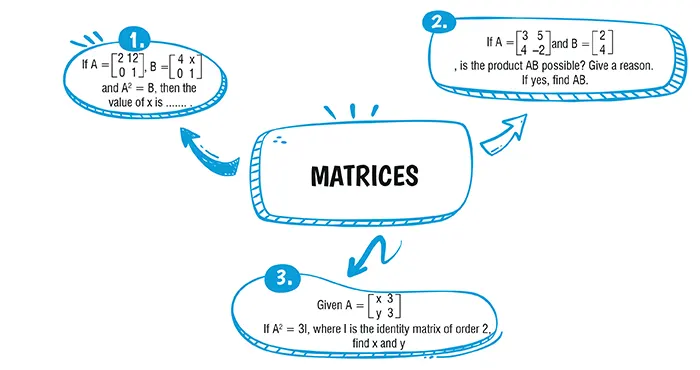
Ans. (c) 36
Explanation:
Let,
$A^2 = B \\ ⇒ A, A,= B \\ ⇒ \begin{bmatrix} 2 & 12 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} 2 & 12 \\ 0 & 1 \end{bmatrix} =\begin{bmatrix} 4 & x \\ 0 & 1 \end{bmatrix}\\ ⇒ \begin{bmatrix} 4 & 36 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 4 & x \\ 0 & 1 \end{bmatrix} \\ ⇒ x = 36$

Q2. If $A = \begin{bmatrix} 2 & -1 \\ 2 & 0 \end{bmatrix}, B = \begin{bmatrix} 1 & 0 \\ 0 & 2 \end{bmatrix} and C = \begin{bmatrix} -3 & 2 \\ 4 & 0 \end{bmatrix},$ then, AB+C=

Options

$(a) \begin{bmatrix} -1 & 0 \\ 6 & 0 \end{bmatrix} \\ (b) \begin{bmatrix} 2 & -2\\ 2 & 0 \end{bmatrix} \\ (c) \begin{bmatrix} 1 & -2 \\ 6 & 0 \end{bmatrix} \\ (d) \begin{bmatrix} -1 & 7 \\ 9 & 0 \end{bmatrix}$

Ans. (a)
Explanation:
we have,
$AB = \begin{bmatrix} 2 & -1 \\ 2 & 0 \end{bmatrix}\begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}\\ =\begin{bmatrix} 2 & -2 \\ 2 & 0 \end{bmatrix} \begin{bmatrix} 2 & -2 \\ 2 & 0 \end{bmatrix} + \begin{bmatrix} -3 & 2 \\ 4 & 0 \end{bmatrix} \\ ∴ AB + C = \begin{bmatrix} -1 & 0 \\ 6 & 0 \end{bmatrix}$

Q3. If A $\begin{bmatrix} 3 & 5 \\ 4 & -2 \end{bmatrix} and B = \begin{bmatrix} 2 \\ 4 \end{bmatrix}$ is the product AB possible ? Give a reason. If yes, find AB.

Explanation:
A $\begin{bmatrix} 3 & 5 \\ 4 & -2 \end{bmatrix}_{2×2} and B = \begin{bmatrix} 2 \\ 4 \end{bmatrix}_{2×1} \\$ The product AB is possible as the number of columns in A is equal to the number of rows in B.
$\text{Now} \space AB = \begin{bmatrix} 3 & 5 \\ 4 & -2\end{bmatrix}\begin{bmatrix} 2\\ 4\end{bmatrix} = \begin{bmatrix} 3×2+5×4\\ 4 × 2 + (-2) × 4\end{bmatrix} = \begin{bmatrix} 26 \\ 0\end{bmatrix}$

Q4. If $A^2= 3I,$ where I is the identity matrix of order 2, find x and y.

Given $A = \begin{bmatrix} x & 3 \\ y & 3 \end{bmatrix}$

Explanation:
Also $A^2= 3I \\ \Rightarrow \begin{bmatrix} x & 3 \\ y & 3 \end{bmatrix}\begin{bmatrix} x & 3 \\ y & 3 \end{bmatrix} = 3 \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\ \Rightarrow \begin{bmatrix} x^2+3y & 3x+9 \\ xy+3y & 3y+9 \end{bmatrix} = \begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix} \\ \text{Comparing both sides,} \\ \text{we get,} \\ 3x + 9 = 0 \\ ⇒ x = -\frac{9}{3} \\ = -3 \space and \space 3y + 9 = 3 \\ ⟹ 3y = 3 – 9 = – 6 \\ ⟹ y=-\frac{6}{3}=-2 \\$ ∴ x=−3 and y=−2

Q5. Let A = $\begin{bmatrix} 2 & 1 \\ 0 & -2\end{bmatrix},B =\begin{bmatrix} 4 & 1 \\ -3 & -2\end{bmatrix} and C = \begin{bmatrix} -3 & 2 \\ -1 & 4\end{bmatrix} \text{Determinde} \space A^2+AC-5B$

Explanation:
LET A= $\begin{bmatrix} 2 & 1 \\ 0 & -2\end{bmatrix}, B= \begin{bmatrix} 4 & 1 \\ -3 & -2\end{bmatrix} and C= \begin{bmatrix} -3 & 2 \\ -1 & 4\end{bmatrix} \\ A^2 = \begin{bmatrix} 2 & 1 \\ 0 & -2\end{bmatrix}\begin{bmatrix} 2 & 1 \\ 0 & -2\end{bmatrix} = \begin{bmatrix} 4+0 & 2-2 \\ 0 & 0+4\end{bmatrix} = \begin{bmatrix} 4 & 0 \\ 0 & 4\end{bmatrix} \\ 5B= \begin{bmatrix} 20 & 5 \\ -15 & -10\end{bmatrix} \\ AC = \begin{bmatrix} 2 & 1 \\ 0 & -2\end{bmatrix}\begin{bmatrix} -3 & 2 \\ -1 & 4\end{bmatrix} =\begin{bmatrix} -6-1 & 4+4 \\ 0+2 & 0-8\end{bmatrix} = \begin{bmatrix} -7 & 8 \\ 2 & -8\end{bmatrix} \\ ∴ A^2+ AC – 5B \\ =\begin{bmatrix} 4 & 0 \\ 0 & 4 \end{bmatrix} + \begin{bmatrix} -7 & 8 \\ 2 & -8 \end{bmatrix} - \begin{bmatrix} 20 & -5 \\ 2 & -8 \end{bmatrix} \\ = \begin{bmatrix} 4-7-20 & 0+8-5 \\ 0+2+15 & 4-8+10 \end{bmatrix} = \begin{bmatrix} -23 & 3 \\ 17 & 6 \end{bmatrix}$

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Want to Practice Mock Tests of this chapter

Download Important Questions of this chapter

ICSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Goods and Service Tax (GST)
Chapter 2	Banking
Chapter 3	Shares and Dividends
Chapter 4	Linear inequations
Chapter 5	Quadratic Equations in one variable
Chapter 6	Ratio and proportion
Chapter 7	Factorization
Chapter 8	Matrices
Chapter 9	Arithmetic Progression
Chapter 10	Geometric Progression
Chapter 11	Coordinate Geometry
Chapter 12	Reflection
Chapter 13	Similarity
Chapter 14	Loci
Chapter 15	Circles
Chapter 16	Constructions
Chapter 17	Mensuration
Chapter 18	Trigonometry
Chapter 19	Statistics
Chapter 20	Probability

Conclusion

The study of matrices class 10 ICSE is both essential and versatile, finding practical applications across diverse fields. Matrices, organized arrays of numbers in rows and columns, serve as a potent tool for equation solving, data manipulation, and geometric transformations. In this chapter, students have delved into the foundational concepts of matrices, grasping their structure, elements, operations, and real-world uses. They’ve acquired proficiency in matrix operations like addition, subtraction, and multiplication, comprehending the governing rules. If you’re aiming to boost your proficiency by practicing more and gaining a thorough grasp of the chapter’s content, oswal.io provides a comprehensive array of matrices class 10 ICSE questions to assist you in your pursuit of a deeper understanding of the subject matter.

Frequently Asked Questions

Q1. What is a matrix?

Ans: A matrix is an ordered arrangement of numbers or symbols in rows and columns.

Q2. What are the dimensions of a matrix?

Ans: The dimensions of a matrix are given as “m × n,” where “m” represents the number of rows, and “n” represents the number of columns.

Q3. How is matrix addition performed?

Ans: Matrix addition is done by adding corresponding elements of two matrices of the same dimensions.

Q4. How do you determine the order of a matrix, and what does it signify?

Ans: The order of a matrix is determined by its dimensions, specified as “number of rows x number of columns” (m x n). It signifies the size and structure of the matrix, crucial for various matrix operations and calculations in linear algebra. For example, a “3 x 2” matrix has 3 horizontal rows and 2 vertical columns.

Q5. How are matrix multiplications carried out?

Ans: Matrix multiplication involves multiplying rows of the first matrix by columns of the second matrix, following specific rules.

Chapter Wise Important Questions for ICSE Board Class 10 Mathematics
Goods and Service Tax (GST)
Banking
Shares and Dividends
Linear inequations
Quadratic Equations in one variable
Ratio and proportion
Factorization
Matrices
Arithmetic Progression
Geometric Progression
Coordinate Geometry
Reflection
Similarity
Loci
Circles
Constructions
Mensuration
Trigonometry
Statistics
Probability

Class 10 Maths Chapter 8 Matrices Important Questions