Factorization

Home / Board / ICSE / important Questions / Class 10 / Maths /Factorization

Class 10 Maths Chapter 7
Factorization
Important Questions

Class 10 Mathematics Chapter 7, Factorization is a crucial topic in ICSE Class 10 mathematics. It involves breaking down algebraic expressions or numbers into their constituent factors. Understanding factorization is essential as it forms the foundation for many other mathematical concepts. Here are some factorisation class 10 ICSE important questions.

Table of Contents

Introduction

Factorization as we study in factorisation class 10 ICSE is the process of expressing a number or algebraic expression as the product of its factors. Factors are numbers or expressions that multiply together to yield the original number or expression. The main goal of factorization is to simplify complex expressions, solve equations, and understand the underlying structure of mathematical concepts.
Common Factorization Techniques:
Common Factors: Identifying and factoring out the common factors shared by multiple terms in an expression.
Example: Factorize 6x + 9y. The common factor is 3, so the expression becomes 3(2x + 3y).
Difference of Squares: Recognizing expressions in the form of

a^2 - b^2

and factoring them as (a + b)(a – b).
Example: Factorize

x^2

– 9. The expression factors as (x + 3)(x – 3).

What is Factorization?

In ICSE Class 10 mathematics, factorization refers to the process of expressing an algebraic expression or a number as the product of its constituent factors. Factors are numbers or algebraic expressions that, when multiplied together, result in the original expression or number. Factorization is an essential skill in mathematics and is used to simplify expressions, solve equations, and understand the underlying structure of mathematical concepts. For example, consider the algebraic expression

2x^2 + 4x

. Factorization of this expression involves finding two expressions that, when multiplied, result in

2x^2 + 4x.

In this case, the factors are 2x and (x + 2), so the factorization is:

2x^2 + 4x = 2x(x + 2).

‍ Factorization is also used to break down numbers into their prime factors. For instance, the prime factorization of the number 12 is: 12 = 2 * 2 * 3.

Class 10 Factorization Important Questions and Answers

Q1. What is the remainder, if we divide $6x^3+ x^2 - 2x + 4$ by x – 2 ?

Options

(a) 48
(b) 52
(c) -26
(d) -24

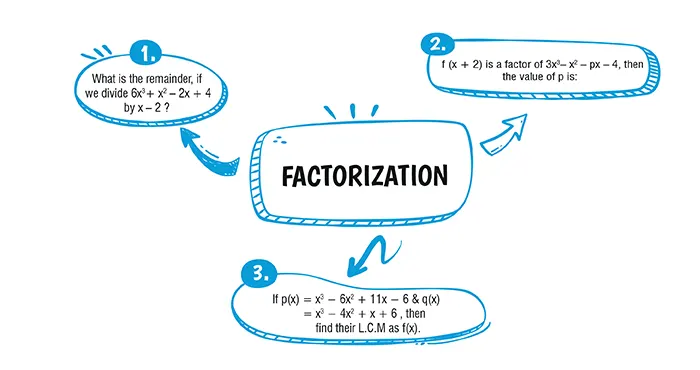
Ans. (b) 52
Explanation:
Let,
$p(x) = 6x^3+ x^2 – 2x + 4 \\ \text{When,} \\ \text{p(x) is divided by x – 2,} \\ \text{Remainder = p(x = 2)} \\ = 6(2)^3 + (2)^2– 2(2) + 4 \\$ = 48 + 4 – 4 + 4 = 52

Q2. f (x + 2) is a factor of $3x^3 - x^2 - px - 4,$ then the value of p is:

Options

(a) 14
(b) 12
(c) 10
(d) 16

Ans. (d) 16
Explanation:
Let,
$f(x) = 3x^3– x^2 – px – 4 \space \space ...(i) \\ \text{Since, (x + 2) is a factor of f(x), f(–2) = 0} \\ ⇒ 3(–2)^3 – (–2)^3 – p(–2) – 4 = 0 \\$ ⇒ –24 – 4 + 2p – 4 = 0
⇒ 2p = 32
⇒ p = 16

Q3. If x – 2 is a factor of $2x^3 - x^2 - px - 2.$

(i) find the value of p
(ii) with the value of p, factorize the above expression completely.

Explanation:
Given expression is $2x^3 - x^2 - px - 2$ and x – 2 is the factor.
(i) x – 2 = 0, x = 2 in expression
$\\2 (2)^3 – (2)^2 – p (2) – 2 = 0\\$ ⇒ 16 – 4 – 2p – 2 = 0
⇒ 10 – 2p = 0
⇒ p = 5
(ii) Putting the value of p‍‍

∴ 2x^3 – x^2 – 5x – 2 = (x – 2) (2x^2 + 3x + 1) \\

The expression can be the written as

(2x^3 + x^2 + 1) (x - 2)

or (2x + 1) (x + 1) (x – 2).‍

Q4. If $𝑝(𝑥) = x^3 − 6 x^2 + 11𝑥 − 6 \space \& \space 𝑞(𝑥) = x^3 − 4x^2 + 𝑥 + 6 ,$ then

(i) find their L.C.M as 𝑓(𝑥).
(ii) and find their H.C.F as 𝑔(𝑥).
(iii) hence prove that: 𝑝(𝑥). 𝑞(𝑥) = 𝑓(𝑥). 𝑔(𝑥)

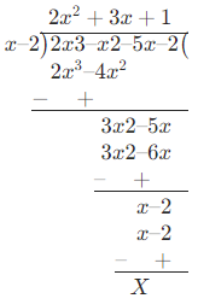
Explanation:
(i) For p (x), we have to find all possible factors of the constant -6
(By factor theorem, we have:)
Factors of - 6 are ∓1, ∓2, ∓3, ∓6, etc. and on putting the value in p (x) we get:
By hit and trial: for x = 1 we get $p(i) = 13 - 6(1)^2 +11(1)-6 = 0.$ Which clearly shows that (x-1) is a factor of p (x).
∴ on dividing p(x) by (x-1)will give:

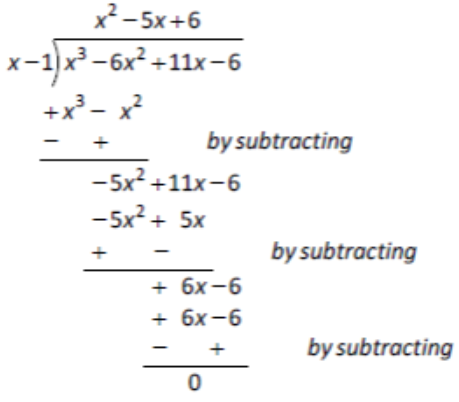
Clearly $p(x) = (x - 1)(x^2 - 5x + 6)$ which on further factorisation gives:
p(x)=(x - 1)(x - 2)(x - 3)...(A)
Similarly solving for q(x) we have:
q(x)=(x - 2)(x - 3)(x - 1)...(B)
∴ L.C.M. = (x - 1)(x - 2)(x - 3)(x + 1)...(c)

Q5. The expression $2x^3 + ax^2 + bx - 2$ leaves the remainder 7 and 0 when divided by (2x – 3) and (x + 2) respectively calculate the value of a and b. With these value of a and b factorise the expression completely.

Explanation:
Let,
$P (x) = 2x^3 + ax^2 + bx – 2 \\ \text{when} \\ \text{P(x) is divided by 2x – 3}\\ P\begin{pmatrix} \frac{3}{2} \end{pmatrix} =2 \begin{pmatrix} \frac{3}{2} \end{pmatrix}^3 +a \begin{pmatrix} \frac{3}{2} \end{pmatrix}^2 +b \begin{pmatrix} \frac{3}{2} \end{pmatrix} -2 = 7 \\ = \frac{27}{4} + \frac{9}{4} a + \frac{3}{2} b - 2 = 7$ = 9a + 6b = 28 + 8 – 27
= 9a + 6b = 9
= 3a + 2b = 3 …(i)
Similarly when P(x) is divided by x + 2
⇒ x = – 2
$∴ 2(- 2)3 + a(- 2)2 + b(- 2) - 2 = 0$ ⇒ – 16 + 4a – 2b – 2 = 0
⇒ 4a – 2b = 18 …(ii)
On solving equations (i) and (ii)
3a + 2b = 3
$\underline{4a – 2b = 18}$ (On adding (ii)
7a = 21
a = 3
On substituting value of a in equation (i)
3 × 3 + 2b = 3
2b = 3 – 9
$b =\frac{-6}{2}$ =-3b = – 3a = 3, b = – 3
On substituting value of a and b
$2x^3 + 3x^2 - 3x - 2$ When x + 2 is a factor

2x^2 - x - 1 = 2x^2 - 2x + x - 1

= 2x(x – 1) + 1 (x – 1)
= (x – 1) (2x + 1)
Hence, required factors are
(x – 1) (x + 2) (2x + 1)

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

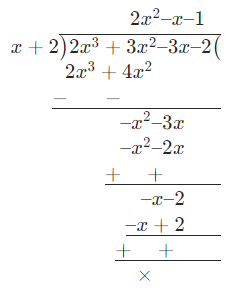
Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Want to Practice Mock Tests of this chapter

Download Important Questions of this chapter

ICSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Goods and Service Tax (GST)
Chapter 2	Banking
Chapter 3	Shares and Dividends
Chapter 4	Linear inequations
Chapter 5	Quadratic Equations in one variable
Chapter 6	Ratio and proportion
Chapter 7	Factorization
Chapter 8	Matrices
Chapter 9	Arithmetic Progression
Chapter 10	Geometric Progression
Chapter 11	Coordinate Geometry
Chapter 12	Reflection
Chapter 13	Similarity
Chapter 14	Loci
Chapter 15	Circles
Chapter 16	Constructions
Chapter 17	Mensuration
Chapter 18	Trigonometry
Chapter 19	Statistics
Chapter 20	Probability

Conclusion

The chapter factorization class 10 ICSE is a foundational and pivotal topic that serves as a cornerstone for various mathematical concepts and practical applications. Mastering these factorisation class 10 ICSE important questions equips you with valuable problem-solving skills for everyday situations, making it a crucial part of your math education.

Chapter Wise Important Questions for ICSE Board Class 10 Mathematics
Goods and Service Tax (GST)
Banking
Shares and Dividends
Linear inequations
Quadratic Equations in one variable
Ratio and proportion
Factorization
Matrices
Arithmetic Progression
Geometric Progression
Coordinate Geometry
Reflection
Similarity
Loci
Circles
Constructions
Mensuration
Trigonometry
Statistics
Probability

Class 10 Maths Chapter 7
Factorization
Important Questions

Introduction

What is Factorization?

Class 10 Factorization Important Questions and Answers

Q1. What is the remainder, if we divide $6x^3+ x^2 - 2x + 4$ by x – 2 ?

Options

(a) 48
(b) 52
(c) -26
(d) -24

Q2. f (x + 2) is a factor of $3x^3 - x^2 - px - 4,$ then the value of p is:

Options

(a) 14
(b) 12
(c) 10
(d) 16

Q3. If x – 2 is a factor of $2x^3 - x^2 - px - 2.$

(i) find the value of p
(ii) with the value of p, factorize the above expression completely.

Q4. If $𝑝(𝑥) = x^3 − 6 x^2 + 11𝑥 − 6 \space \& \space 𝑞(𝑥) = x^3 − 4x^2 + 𝑥 + 6 ,$ then

(i) find their L.C.M as 𝑓(𝑥).
(ii) and find their H.C.F as 𝑔(𝑥).
(iii) hence prove that: 𝑝(𝑥). 𝑞(𝑥) = 𝑓(𝑥). 𝑔(𝑥)

Q5. The expression $2x^3 + ax^2 + bx - 2$ leaves the remainder 7 and 0 when divided by (2x – 3) and (x + 2) respectively calculate the value of a and b. With these value of a and b factorise the expression completely.

ICSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. What is factorization, and why is it important in mathematics?

Q2. What are prime factors, and how do you find them?

Q3. What is the difference between algebraic and numerical factorization?

Q4. How do you factorize a quadratic trinomial like $ax^2 + bx + c?$

Q5. What is a perfect square trinomial, and how is it factorized?

Class 10 Maths Chapter 7 Factorization Important Questions

Introduction

What is Factorization?

Class 10 Factorization Important Questions and Answers

Q1. What is the remainder, if we divide 6x^3+ x^2 – 2x + 4 by x – 2 ?

Options

(a) 48(b) 52(c) -26(d) -24

Q2. f (x + 2) is a factor of 3x^3 – x^2 – px – 4, then the value of p is:

Options

(a) 14(b) 12(c) 10(d) 16

Q3. If x – 2 is a factor of 2x^3 – x^2 – px – 2.

(i) find the value of p(ii) with the value of p, factorize the above expression completely.

Q4. If 𝑝(𝑥) = x^3 − 6 x^2 + 11𝑥 − 6 \space \& \space 𝑞(𝑥) = x^3 − 4x^2 + 𝑥 + 6 , then

(i) find their L.C.M as 𝑓(𝑥). (ii) and find their H.C.F as 𝑔(𝑥). (iii) hence prove that: 𝑝(𝑥). 𝑞(𝑥) = 𝑓(𝑥). 𝑔(𝑥)

Q5. The expression 2x^3 + ax^2 + bx – 2 leaves the remainder 7 and 0 when divided by (2x – 3) and (x + 2) respectively calculate the value of a and b. With these value of a and b factorise the expression completely.

ICSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. What is factorization, and why is it important in mathematics?

Q2. What are prime factors, and how do you find them?

Q3. What is the difference between algebraic and numerical factorization?

Q4. How do you factorize a quadratic trinomial like ax^2 + bx + c?

Q5. What is a perfect square trinomial, and how is it factorized?

Class 10 Maths Chapter 7
Factorization
Important Questions

Q1. What is the remainder, if we divide $6x^3+ x^2 - 2x + 4$ by x – 2 ?

(a) 48
(b) 52
(c) -26
(d) -24

Q2. f (x + 2) is a factor of $3x^3 - x^2 - px - 4,$ then the value of p is:

(a) 14
(b) 12
(c) 10
(d) 16

Q3. If x – 2 is a factor of $2x^3 - x^2 - px - 2.$

(i) find the value of p
(ii) with the value of p, factorize the above expression completely.

Q4. If $𝑝(𝑥) = x^3 − 6 x^2 + 11𝑥 − 6 \space \& \space 𝑞(𝑥) = x^3 − 4x^2 + 𝑥 + 6 ,$ then

(i) find their L.C.M as 𝑓(𝑥).
(ii) and find their H.C.F as 𝑔(𝑥).
(iii) hence prove that: 𝑝(𝑥). 𝑞(𝑥) = 𝑓(𝑥). 𝑔(𝑥)

Q5. The expression $2x^3 + ax^2 + bx - 2$ leaves the remainder 7 and 0 when divided by (2x – 3) and (x + 2) respectively calculate the value of a and b. With these value of a and b factorise the expression completely.

Q4. How do you factorize a quadratic trinomial like $ax^2 + bx + c?$