logo
Log in
logo
Log in
Start Free Trial
Linear Programming

Home / Boards / CBSE / Important Questions / Class 12 / Maths / Linear Programming

Class 12 Maths Chapter 12
Linear Programming
Important Questions

exam preparation with oswal.io
Linear Programming” typically deals with a branch of mathematics and operations research that is used to find the best possible solution or outcome in a given mathematical model. The model’s requirements are represented by linear relationships. questions related to Chapter 812 on Linear programming for Class 12 Mathematics. Crafted specifically to aid students in preparing for the CBSE Class 12 Mathematics Examination 2024–25, these questions cover vital aspects of the topic. Engaging with various question formats enhances students’ readiness for the exams

Introduction

Linear programming is a mathematical method used for finding the best possible solution to a problem that involves multiple linear relationships. This technique is widely used in business, economics, engineering, and the military, among other fields, to optimize the use of resources under given constraints.Linear programming is a powerful tool for decision-making and resource optimization in a wide range of fields. Its ability to provide clear, quantitative solutions to complex problems with multiple interacting factors makes it an invaluable technique in the modern world. Understanding the basics of linear programming opens up a world of possibilities for efficiently solving diverse real-world problems.

What are Linear Programming?

Linear programming is a mathematical technique used for optimizing a linear objective function, subject to a set of linear equality or inequality constraints. This method is extensively used in various fields such as business, economics, engineering, and military applications to make the most efficient use of limited resources. Linear programming (LP) is a mathematical technique used for optimization, where the goal is to find the best outcome (such as maximum profit or lowest cost) in a given mathematical model. Its functions are linear in nature. This method is widely used in business, economics, and engineering to efficiently allocate resources under a set of constraints.

Class 12 Linear Programming Important Questions and Answers

Q1. Infeasibility means that the number of solutions to the linear programming models that satisfies all constraints is :
Options
(a) At least
(b) An infinite number
(c) Zero
(d) At least 2

Ans. (c) Zero
Explanation:
As not all the constraints are satisfied. That is why, no solution exist or is infeasible.

Q2. Which of the term is not used in a linear programming problem?
Options
(a) Optimal solution
(b) Feasible solution
(c) Concave region
(d) Objective function

Ans. (c) Concave region
Explanation:
Optimal solution, feasible solution and objective function are the terms used in linear programming problem.

Q3. A furniture manufacturer manufactures two products: chairs and tables. Processing of these products is done on two machines A and B. A chair requires 3 hours on machine A and 5 hours on machine B. A table requires 6 hours on machine A and 2 hours on machine B. There are 15 hours per day available on machine A and 24 hours on machine B. Profit gained by the manufacturer from a chair and a table is ₹ 5 and ₹8 respectively. Formulate the problem as a linear programming problem.

Explanation:
The given data can be put in tabular form as under

Profit₹5₹8
Machine/ProductsChairTableTime available
A3 hrs.6 hrs.15 hrs.
B5 hrs. 2 hrs.24 hrs.

Let x and y number of chairs and tables be produced respectively.
Then, total profit to be maximized
Max z = 5x + 8y
Given, A chair requires 3 hrs. on machine A and A table requires 6 hrs. on machine A. Machine A cannot work for more than 15 hrs.
∴ 3x + 6y ≤ 15
Similarly, A chair requires 5 hrs. and a table requires 2 hrs. on machine B. Machine B can not work for more than 24 hrs.
∴ 5x + 2y ≤ 24
Since the number of chairs and tables can not be negative
∴ x ≥ 0, 1 ≥ 0
Hence, the given LPP is
Max Z = 5x + 8y
Subject to the constraints
3x + 6y ≤ 15
5x + 2y ≤ 24
x ≥ 0 y ≥ 0

Q4. Solve the following linear programming problem graphically: Minimise Z = 200 x + 500 y subject to the constraints:
x + 2y ≥ 10
3x + 4y ≤ 24
x ≥ 0, y ≥ 0

Explanation:
Minimise Z = 200 x + 500 y … (1)
subject to the constraints:
x + 2y ≥ 10 … (2)
3x + 4y ≤ 24 … (3)
x ≥ 0, y ≥ 0 … (4)
Let us draw the graph of x + 2y = 10 and 3x + 4y = 24 as below.

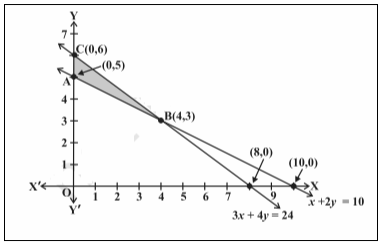
linear programming important questions

The shaded region in the above figure is the feasible region ABC determined by the
system of constraints (2) to (4), which is bounded. The coordinates of corner point A, B and C are (0,5), (4,3) and (0,6) respectively.
Calculation of Z = 200x + 500y at these points.

Corner pointValue of Z
(0, 5)2500
(4, 3)2300← Minimum
(0, 6)3000

Hence, the minimum value of Z is 2300 is at the point (4, 3).

Q5. A manufacturing company makes two types of television sets; one is black and white and the other is colour. The company has resources to make at most 300 sets a week. It takes Rs 1800 to make a black and white set and Rs 2700 to make a coloured set. The company can spend not more than Rs 648000 a week to make television sets. If it makes a profit of Rs 510 per black and white set and Rs 675 per coloured set, how many sets of each type should be produced so that the company has a maximum profit? Formulate this problem as a LPP given that the objective is to maximise the profit.

Explanation:
Let x and y denote, respectively, the number of black and white sets and coloured sets made each week.
Thus x ≥ 0, y ≥ 0
The company can make at most 300 sets a week, therefore, x + y ≤ 300.
Weekly cost (in Rs) of manufacturing the set is 1800x + 2700y and the company can spend up to Rs. 648000.
Therefore, 1800x + 2700y ≤ 648000
or
2x + 3y ≤ 720
The total profit on x black and white sets and y coloured sets is Rs (510x + 675y).
Let the objective function be Z = 510x + 675y.
Therefore, the mathematical formulation of the problem is as follows.
Maximise Z = 510x + 675y subject to the constraints :
x + y ≤ 300
2x + 3y ≤ 720
x ≥ 0, y ≥ 0
The graph of x + y = 30 and 2x + 3y = 720 is given below.

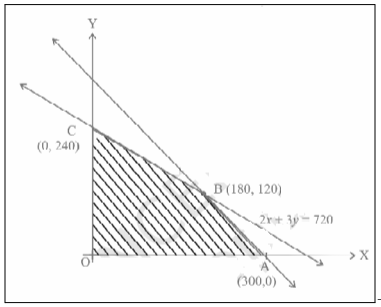
Linear Programming Q5
Corner pointValue of Z
A(300, 0)153000
B(180, 120)172800 = Maximum
C(0, 240)162000

Hence, the maximum profit will occur when 180 black & white sets and 120 coloured sets are produced.

CBSE Class 12 Maths Chapter wise Important Questions

making of global world class 10 important questions

Conclusion

Linear programming provides a systematic approach to solving problems that involve maximizing or minimizing a linear objective function subject to a set of linear constraints. The versatility and efficiency of linear programming make it an indispensable tool in numerous areas, including business, economics, engineering, logistics, and resource management. Exploring Linear programming for Class 12 Mathematics, becomes essential for a comprehensive grasp of this fundamental aspect of mathematics. oswal.io provide class 12 Linear programming important questions and answers.

Frequently Asked Questions

Ans: Linear programming is a mathematical method used to find the best possible outcome (such as maximum profit or minimum cost) in a given model, where the requirements are represented by linear relationships.
Ans: The objective function in linear programming is a linear equation that represents what you are trying to maximize or minimize, such as profit, cost, or time. It’s expressed in terms of decision variables.
Ans: Constraints in linear programming are the limitations or requirements that the solution must satisfy. They are represented as linear inequalities or equations and define the feasible region.
Ans: The feasible region is the set of all possible solutions that satisfy all the constraints of a linear programming problem. It’s typically represented graphically as a polygon or polyhedron.
Ans: Linear programming problems can be solved using various methods, the most common being the graphical method for two-variable problems and the Simplex method for larger problems.
logo
Instagram Linkedin-in Facebook-f Youtube Twitter
logo
Instagram Linkedin-in Facebook-f Youtube Twitter
  • Syllabus
  • Blogs
  • Plans
  • Contact Us
  • Privacy Policy

CBSE Important Questions Class 9

CBSE Important Questions Class 10

CBSE Important Questions Class 12

CBSE Practice Papers

CBSE Practice Papers

ICSE Important Questions Class 9

  • ICSE Class 9 Maths
  • ICSE Class 9 Physics
  • ICSE Class 9 Chemistry
  • ICSE Class 9 Biolog1y
  • ICSE Class 9 History & Civics
  • ICSE Class 9 Geography
  • ICSE Class 9 Computer Applications

ICSE Important Questions Class 10

ICSE Practice Papers

  • ICSE Class 10 Physics
  • ICSE Class 10 Chemistry
  • ICSE Class 10 Biology
  • ICSE Class 10 Maths

ISC Important Questions Class 12

ISC Practice Papers

  • ISC Class 12 Physics
  • ISC Class 12 Chemistry
  • ISC Class 12 Biology
  • ISC Class 12 Maths

Contact Us

Head Office : Ground Floor, 1 / 12 Sahitya Kunj, M.G Road Agra 282002, Uttar Pradesh (India)
Phone No.: +91-562 25277711
Mobile No.: +91-7455077222
Email: support@oswalpublishers.in
Corporate Office : Noida One, B 702, B7, Sector 62,
Noida - 201309, Uttar Pradesh
Phone No.: +91-562 25277711
Mobile No.: +91-75348 77222
Email: support@oswalpublishers.in

© Copyright 2024 oswal.io by OSWAL PUBLISHERS Simplifying Exams